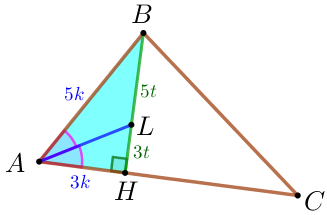
\(\displaystyle ABC\) үшбұрышында \(\displaystyle A\) бұрышының биссектрисасы \(\displaystyle B \) нүктесінен есептей отырып, \(\displaystyle 5:3\) қатынасында \(\displaystyle B\) төбесінен жүргізілген биіктікті бөледі. Егер \(\displaystyle ABC \) үшбұрышына сырттай сызылған шеңбердің радиусы \(\displaystyle 5 \) тең болса, \(\displaystyle BC\) бүйір қабырғасының ұзындығын табыңыз.
Есептің шарты бойынша сызба салайық.
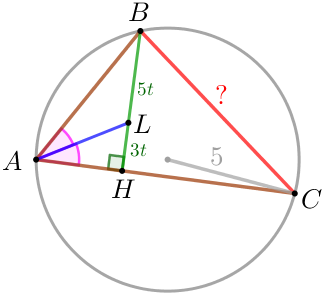 | \(\displaystyle ABC{\small:}\) үшбұрышында
Шарт бойынша \(\displaystyle \frac{BL}{LH}=\frac{5}{3} {\small,}\) \(\displaystyle R=5 \) – \(\displaystyle ABC{\small}\) үшбұрышына сырттай сызылған шеңбердің радиусы \(\displaystyle BC {\small}\) қабырғасының ұзындығын табу қажет |
\(\displaystyle \frac{BC}{\sin \angle A}=2 \cdot R {\small,}\\ \)
\(\displaystyle BC=2 \cdot R \cdot \sin \angle A {\small,}\\ \)
\(\displaystyle BC=2 \cdot 5 \cdot \sin \angle A =10 \cdot \sin \angle A{\small.}\\ \)
\(\displaystyle \sin \angle A{\small}\) табу қажет
Тікбұрышты \(\displaystyle ABH{\small}\) үшбұрышын қарастырайық
|
|
\(\displaystyle \frac{AH}{AB}=\frac{LH}{BL}=\frac{3}{5} {\small.}\)
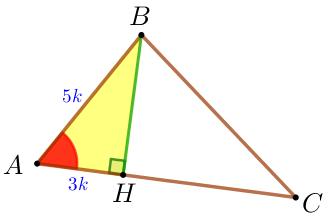 | Тікбұрышты үшбұрыштағы сүйір бұрыш үшін іргелес катеттің гипотенузаға қатынасы сол бұрыштың косинусына тең болғандықтан, онда \(\displaystyle \cos \angle A = \frac{AH}{AB}=\frac{3}{5} {\small.}\) Негізгі тригонометриялық тепе-теңдік бойынша: \(\displaystyle (\sin \angle A)^2+(\cos \angle A)^2=1{\small.}\) |
Сонда
\(\displaystyle (\sin \angle A)^2=1-(\cos \angle A)^2=1- \bigg(\frac{3}{5}\bigg)^2=1-\frac{9}{25}=\frac{25-9}{25}=\frac{16}{25}= \bigg(\frac{4}{5}\bigg)^2{\small.}\\ \)
Яғни, \(\displaystyle \sin \angle A= \frac{4}{5} {\small.}\)
Төмендегіні аламыз
\(\displaystyle BC=10 \cdot \sin \angle A=10 \cdot \frac{4}{5}=8{\small.} \)
Жауабы: \(\displaystyle 8 {\small.}\)