Решите неравенство
\(\displaystyle x^2 - 3x -4<0{\small ,}\)
если известен график соответствующей квадратичной функции.
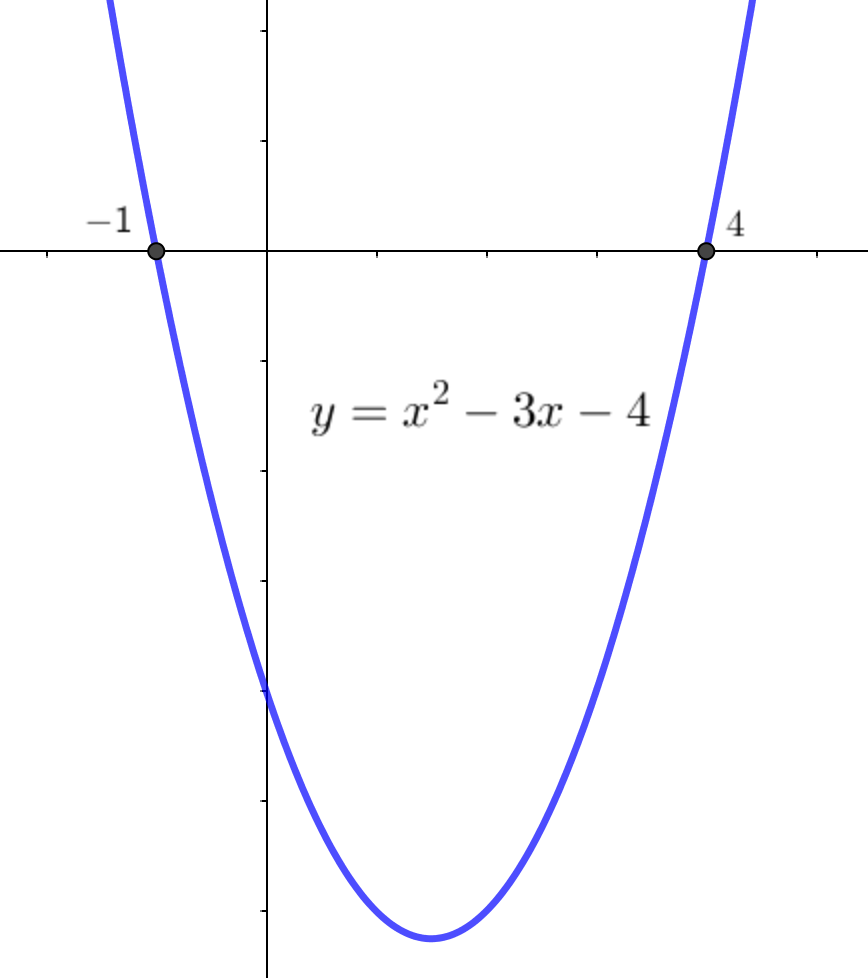
Для решения неравенства \(\displaystyle x^2 - 3x -4<0\) надо найти те значения \(\displaystyle x{ \small ,} \) которые дают значение \(\displaystyle x^2 - 3x -4 \) меньше нуля.
Для параболы \(\displaystyle y=x^2 - 3x -4 \) это означает, что надо найти те значения \(\displaystyle x{ \small ,} \) для которых \(\displaystyle y \) меньше нуля.
То есть нужно определить те \(\displaystyle x{ \small ,} \) для которых соответствующие точки параболы лежат ниже оси \(\displaystyle \rm OX {\small . }\)
Выделим красным цветом точки параболы, лежащие ниже оси \(\displaystyle \rm OX {\small : }\)
Определим координаты \(\displaystyle x\) данных точек:
Получаем, что это точки, лежащие между точек пересечения параболы с осью \(\displaystyle \rm OX\) (без точек пересечения, так как в них \(\displaystyle x^2 - 3x -4=0\)).
То есть это все точки между \(\displaystyle -1 \) и \(\displaystyle 4{\small :}\)
Таким образом, решение неравенства на прямой выглядит следующим образом:
На прямой изображены все точки, координата \(\displaystyle x \) которых больше \(\displaystyle -1 \) и меньше \(\displaystyle 4{ \small .} \)
То есть это все точки, для которых \(\displaystyle -1<x<4{\small .} \)
Переписывая это в виде интервала, получаем:
\(\displaystyle x\in (-1;\, 4){\small .}\)
Ответ: \(\displaystyle x\in (-1;\, 4){\small .}\)