В треугольнике \(\displaystyle ABC\) угол \(\displaystyle C\) равен \(\displaystyle 90^{\circ}{\small , }\) длина сторон \(\displaystyle AB=10 {\small , }\) \(\displaystyle BC=6 {\small .}\) Найдите площадь треугольника.

Площадь прямоугольного треугольника равна половине произведения длин катетов:
\(\displaystyle S_{ABC}=\frac{1}{2}\cdot AC\cdot BC{\small .}\)
Найдем сторону \(\displaystyle AC{\small .}\)
По теореме Пифагора имеем: \(\displaystyle AC^2+BC^2=AB^2{\small .}\) Подставляя \(\displaystyle AB=10\) и \(\displaystyle BC=6\) в равенство, получаем: \(\displaystyle AC^2+6^2=10^2{\small , }\) \(\displaystyle AC^2+36=100{\small , }\) \(\displaystyle AC^2=100-36=64{\small , }\) Поскольку длина отрезка положительна, то \(\displaystyle AC=8{\small . }\) | 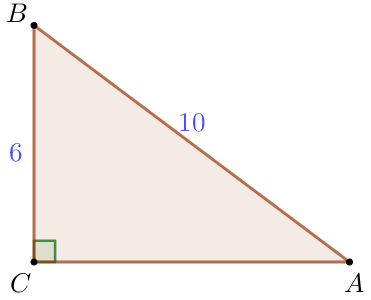 |
Подставим \(\displaystyle AC=8\) и \(\displaystyle BC=6\) в формулу площади прямоугольного треугольника:
\(\displaystyle S_{ABC}=\frac{1}{2}\cdot 8\cdot 6{\small , }\)
\(\displaystyle S_{ABC}=24{\small .}\)
Ответ: \(\displaystyle 24{\small .}\)