Биссектрисы углов \(\displaystyle A\) и \(\displaystyle D\) параллелограмма \(\displaystyle ABCD\) пересекаются в точке \(\displaystyle M {\small,}\) лежащей на стороне \(\displaystyle BC {\small.}\)
\(\displaystyle a) \)Докажите, что точка \(\displaystyle M\) равноудалена от прямых \(\displaystyle AB {\small,}\) \(\displaystyle AD\) и \(\displaystyle CD {\small.}\)
\(\displaystyle б) \) Найдите высоту параллелограмма, проведённую к стороне \(\displaystyle AB {\small,}\) если расстояние от точки \(\displaystyle M\) до прямой \(\displaystyle AD\) равно \(\displaystyle 9{\small.}\)
\(\displaystyle a) \)Выполним построение по условию задачи.
 | \(\displaystyle ABCD\) – параллелограмм. \(\displaystyle AM\) – биссектриса угла \(\displaystyle A{\small.}\) \(\displaystyle DM\) – биссектриса угла \(\displaystyle D{\small.}\) Точка \(\displaystyle M\) лежит на стороне \(\displaystyle BC{\small.}\) |
Требуется доказать, что точка \(\displaystyle M\) равноудалена от прямых \(\displaystyle AB {\small,}\) \(\displaystyle AD\) и \(\displaystyle CD {\small.}\)
То есть доказать, что равны расстояния от точки \(\displaystyle M\) до прямых \(\displaystyle AB {\small,}\) \(\displaystyle AD\) и \(\displaystyle CD {\small.}\)
Расстояние от точки до прямой – это длина перпендикуляра, опущенного из данной точки на прямую. Перпендикуляр – это кратчайшее расстояние от точки до прямой.
Выполним дополнительные построения.
Из точки \(\displaystyle M\) проведём перпендикуляры к прямым \(\displaystyle AB {\small,}\) \(\displaystyle AD\) и \(\displaystyle CD {\small.}\)
 | \(\displaystyle MH \perp AB {\small;}\) \(\displaystyle MK \perp AD {\small;}\) \(\displaystyle MP \perp CD{\small.}\) Докажем, что \(\displaystyle MH=MK=MP{\small.}\) |
Рассмотрим прямоугольные треугольники \(\displaystyle AMH\) и \(\displaystyle AMK{\small.}\)
Следовательно, \(\displaystyle \triangle AMH=\triangle AMK\) по гипотенузе и острому углу. В равных треугольниках соответственные стороны равны. Значит, \(\displaystyle MH=MK{\small.}\) |  |
Рассмотрим прямоугольные треугольники \(\displaystyle DMK\) и \(\displaystyle DMP{\small.}\)
Следовательно, \(\displaystyle \triangle DMK=\triangle DMP\) по гипотенузе и острому углу. В равных треугольниках соответственные стороны равны. Значит, \(\displaystyle MK=MP{\small.}\) |  |
Получили
\(\displaystyle MH=MK=MP{\small.}\)
Следовательно, точка \(\displaystyle M\) равноудалена от прямых \(\displaystyle AB {\small,}\) \(\displaystyle AD\) и \(\displaystyle CD {\small.}\)
Утверждение доказано.
\(\displaystyle б)\) По условию задачи расстояние от точки \(\displaystyle M\) до прямой \(\displaystyle AD\) равно \(\displaystyle 9{\small.}\) То есть \(\displaystyle MK=9{\small.}\)
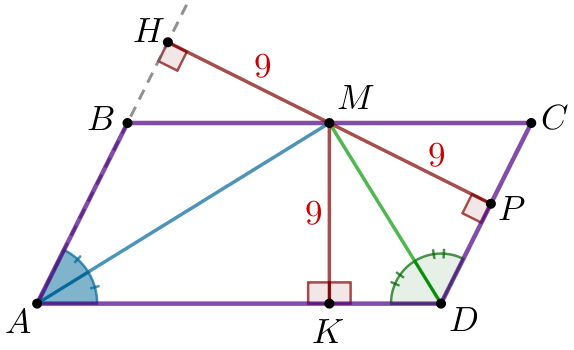 | Высота параллелограмма \(\displaystyle ABCD\), проведенная к стороне \(\displaystyle AB{\small,}\) равна расстоянию между параллельными прямыми \(\displaystyle AB\) и \(\displaystyle CD{\small,}\) то есть длине перпендикуляра \(\displaystyle PH\) (смотри рисунок). \(\displaystyle PH=MP+MH{\small.}\) Так как \(\displaystyle MH=MP=MK=9{\small,}\) то \(\displaystyle PH=9+9=18{\small.}\) |
Следовательно, высота параллелограмма, проведённая к стороне \(\displaystyle AB {\small,}\) равна \(\displaystyle 18{\small.}\)
Ответ: \(\displaystyle б)\ 18 {\small.}\)