Тапсырма
\(\displaystyle y=3x^2{\small :}\)квадраттық функциясының графигін таңдаңыз:
| \(\displaystyle 1\) | 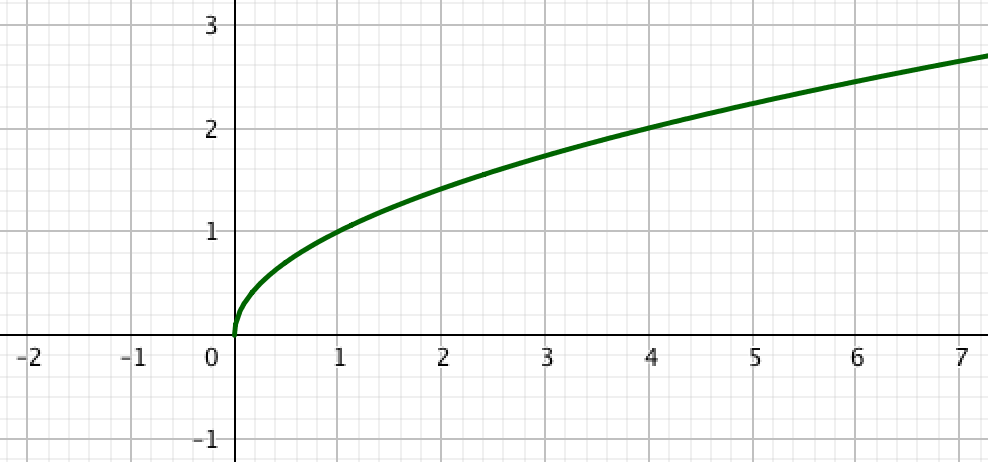 | \(\displaystyle 2\) | 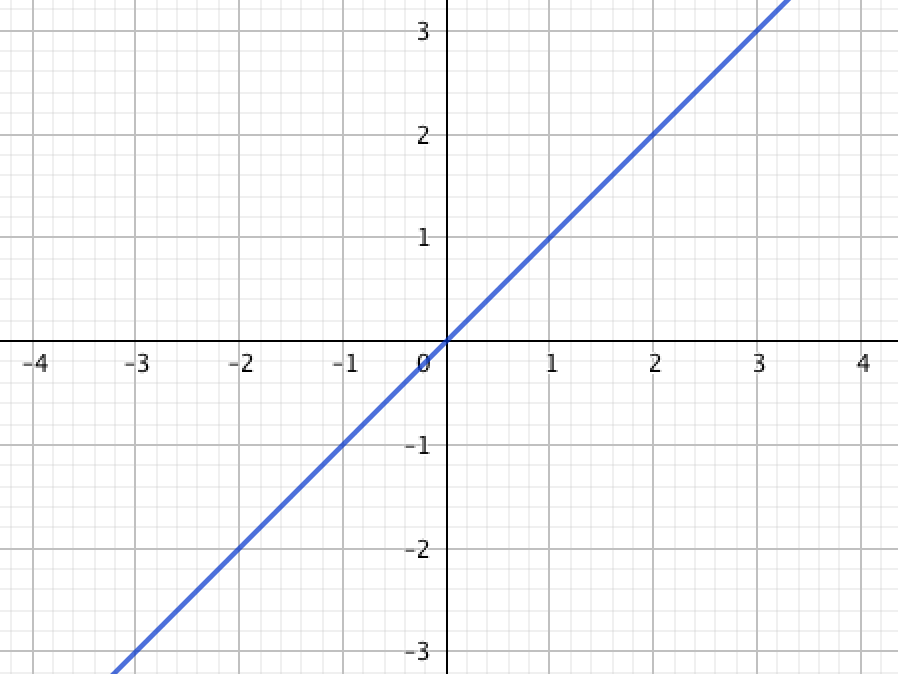 |
| \(\displaystyle 3\) | 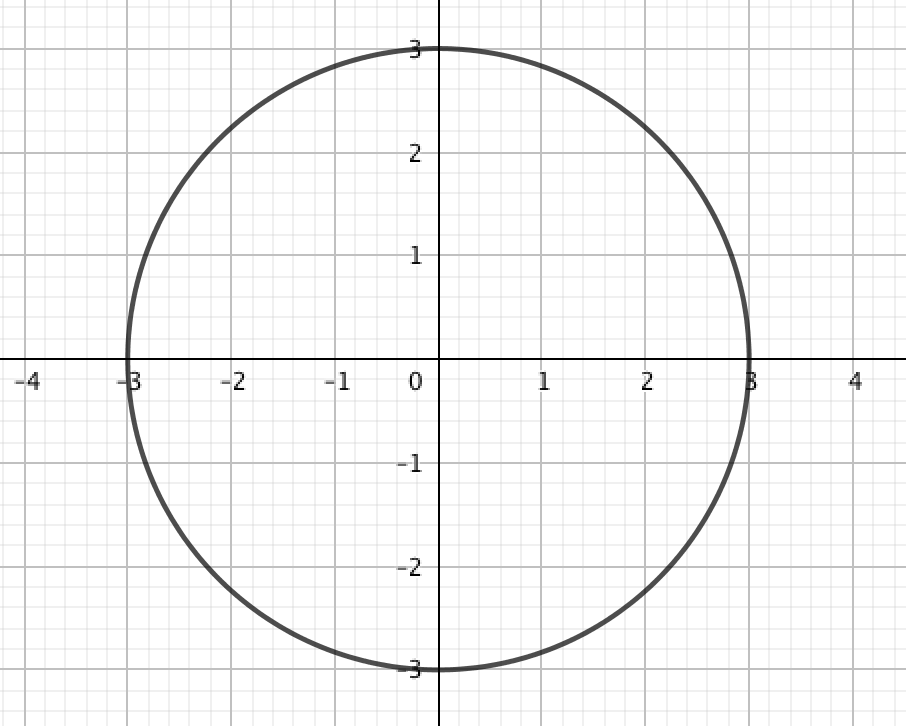 | \(\displaystyle 4\) | 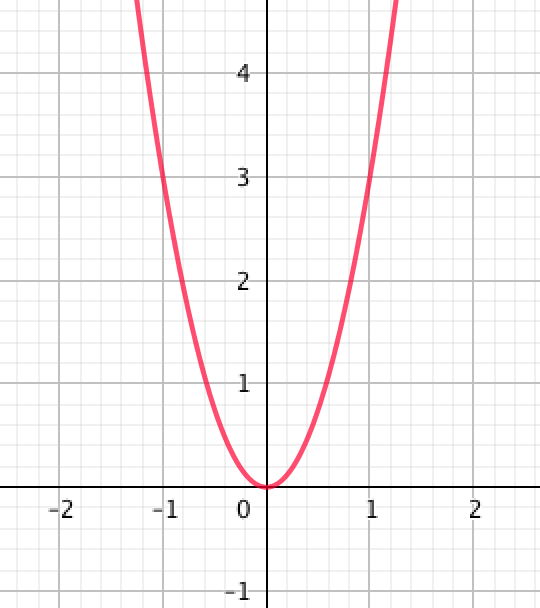 |
Шешім
\(\displaystyle y=3x^2\) квадраттық функциясының графигін нүктелер бойынша құрайық. Ол үшін мәндер кестесін:
| \(\displaystyle x\) | \(\displaystyle 0\) | \(\displaystyle 0{,}2\) | \(\displaystyle 0{,}4\) | \(\displaystyle 0{,}6\) | \(\displaystyle 0{,}8\) | \(\displaystyle 1\) | \(\displaystyle 1{,}2\) |
| \(\displaystyle y=3x^2\) | \(\displaystyle 0\) | \(\displaystyle 0{,}12\) | \(\displaystyle 0{,}48\) | \(\displaystyle 1{,}08\) | \(\displaystyle 1{,}92\) | \(\displaystyle 3\) | \(\displaystyle 4{,}32\) |
және ОХ осі бойынша симметриялы теріс мәндерін құрайық:
| \(\displaystyle x\) | \(\displaystyle -1{,}2\) | \(\displaystyle -1\) | \(\displaystyle -0{,}8\) | \(\displaystyle -0{,}6\) | \(\displaystyle -0{,}4\) | \(\displaystyle -0{,}2\) | \(\displaystyle 0\) |
| \(\displaystyle y=3x^2\) | \(\displaystyle 4{,}32\) | \(\displaystyle 3\) | \(\displaystyle 1{,}92\) | \(\displaystyle 1{,}08\) | \(\displaystyle 0{,}48\) | \(\displaystyle 0{,}12\) | \(\displaystyle 0\) |
Жазықтықтағы берілген нүктелерді белгілейік:
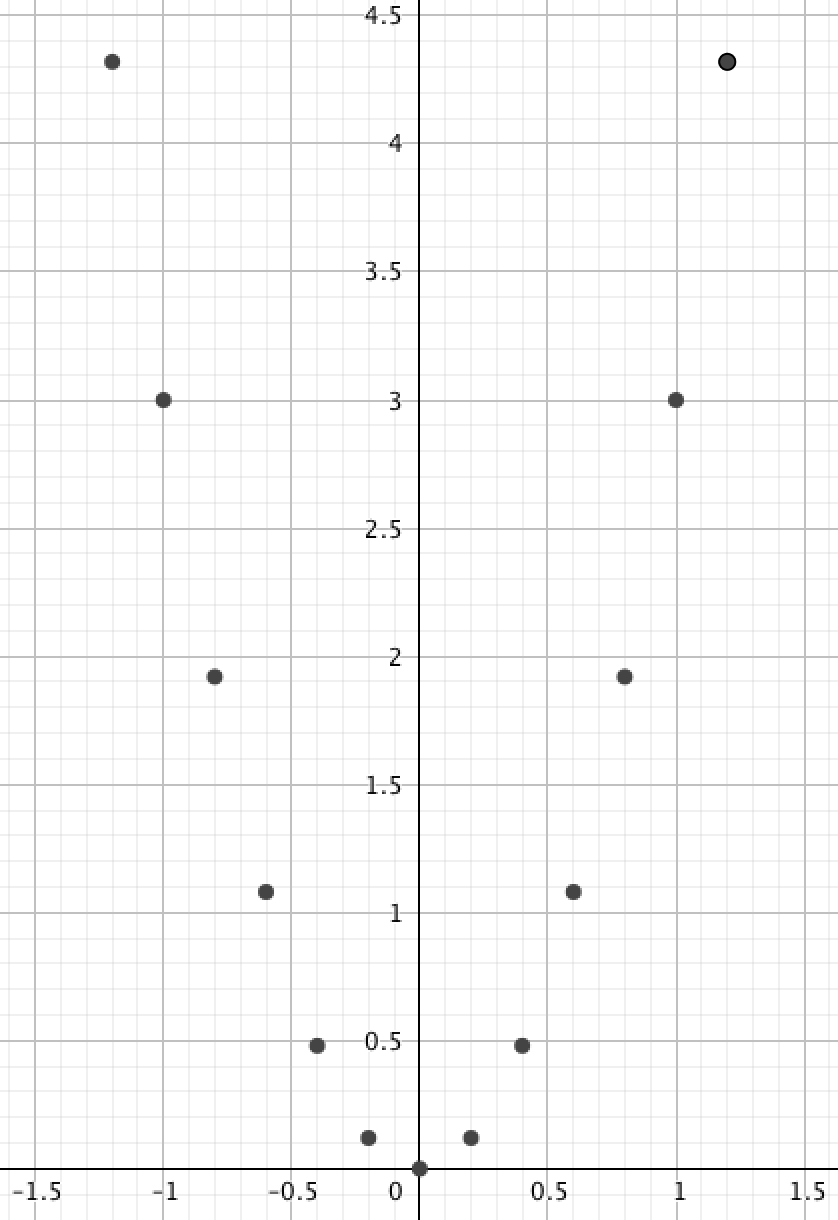
және оларды қосамыз:
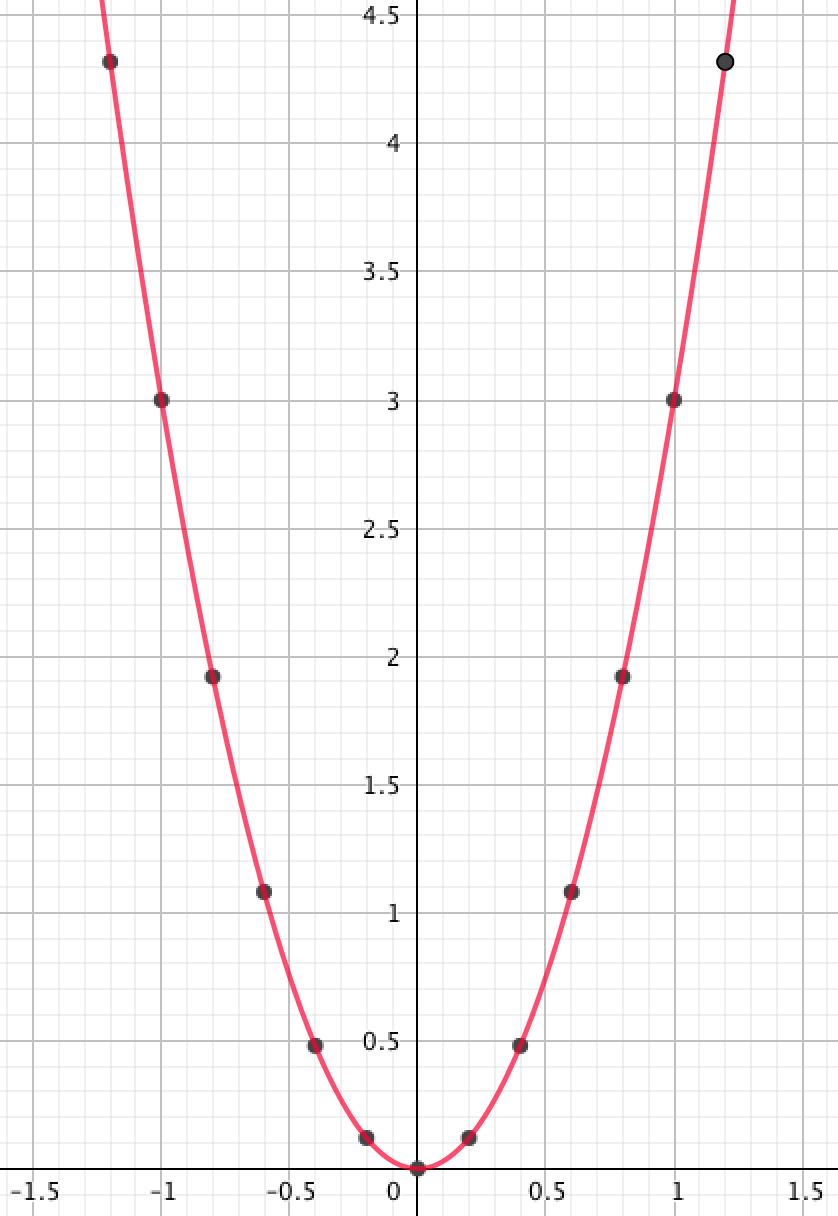
Графиктерді салыстыру арқылы
| \(\displaystyle 1\) |  | \(\displaystyle 2\) |  |
| \(\displaystyle 3\) |  | \(\displaystyle 4\) |  |
\(\displaystyle y=3x^2\) квадраттық функциясының графигі \(\displaystyle 4{\small }\)нұсқаға сәйкес келеді.
Жауабы: \(\displaystyle 4{\small .}\)