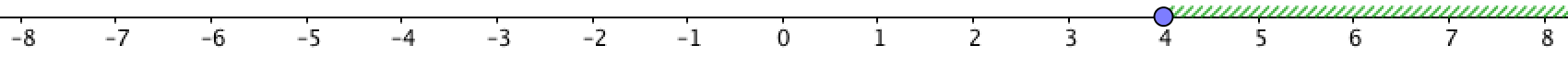Жартылай интервалдар мен жартылай кесінділерге сәйкес келетін нүктелердің геометриялық орнын сызыңыз:
\(\displaystyle (-\infty;\,-4), \qquad (-\infty;\,-4], \qquad (2;+\infty), \qquad [4;+\infty)\)
\(\displaystyle \color{blue}{(-\infty;\,-4)}\)
Анықтама бойынша, \(\displaystyle (-\infty; \,-4)\) – бұл координаттары \(\displaystyle -4{\small }\)-тен кем болатын барлық сандардың жиыны.
Осы аралыққа сәйкес келетін нүктелер келесідей бейнеленген:
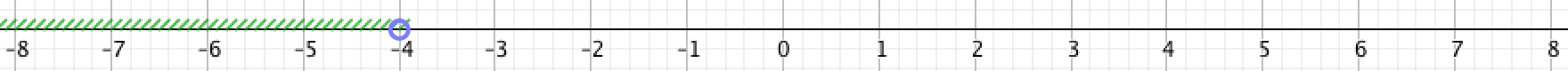
\(\displaystyle \color{blue}{(-\infty;\,-4]}\)
Анықтама бойынша, \(\displaystyle (-\infty; \,-4]\) – \(\displaystyle -4{\small }\) координатасы бар нүктені қоса алғанда координаталары \(\displaystyle -4{\small }\)-тен кем барлық сандар жиыны.
Осы жартылай интервалға сәйкес келетін нүктелер келесідей бейнеленген:

\(\displaystyle \color{blue}{(2;+\infty)}\)
Анықтама бойынша, \(\displaystyle (2;+\infty)\) – бұл координаттары \(\displaystyle 2{\small }\)-ден артық болатын барлық сандардың жиыны.
Осы аралыққа сәйкес келетін нүктелер келесідей бейнеленген:

\(\displaystyle \color{blue}{[4;+\infty)}\)
Анықтама бойынша, \(\displaystyle [4;+\infty)\) – \(\displaystyle 4{\small }\) координатасы бар нүктені қоса алғанда координаталары \(\displaystyle 4{\small }\)-тен артық барлық сандар жиыны
Осы жартылай интервалға сәйкес келетін нүктелер келесідей бейнеленген: