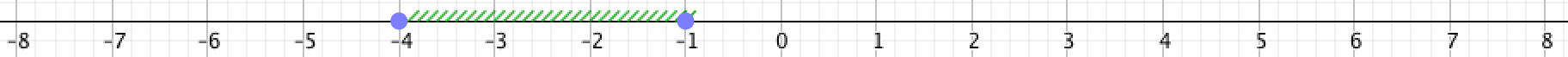Графикте көрсетілген нүктелердің орналасуына сәйкес сандық аралықты жазыңыз:
| \(\displaystyle 1)\) |
|
| \(\displaystyle 2)\) |
|
| \(\displaystyle 3)\) |
|
| \(\displaystyle 4)\) |
|
Суретте \(\displaystyle -4\) қосқанда және \(\displaystyle -1{\small } \) қосқанда, \(\displaystyle -4 \) және \(\displaystyle -1{\small } \) арасындағы барлық нүктелер көрсетілген:
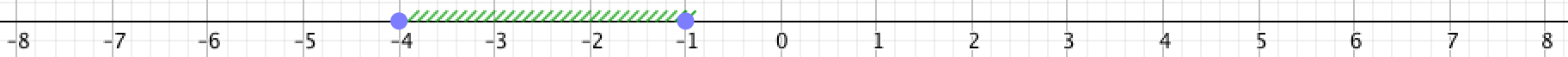
Яғни, координаттары \(\displaystyle -4 \)-тен артық және \(\displaystyle -1{\small }\)-ден кем немесе оған тең барлық нүктелер бейнеленген. Басқаша айтқанда, бұл \(\displaystyle -4\le x \le -1{\small }\) болатын \(\displaystyle x\) координатасы бар барлық нүктелер. Мұндай жиын келесідей белгіленеді: \(\displaystyle [-4{\small ; }\,-1]{\small . } \)
Осылайша, ізделініп отырған сандық аралық:
\(\displaystyle x \in [-4{\small ; }\,-1]{\small . } \)
Жауабы: \(\displaystyle x \in [-4{\small ; }\,-1]{\small . } \)
Суретте \(\displaystyle -1\) қоспағанда және \(\displaystyle 2{\small } \) қоспағанда \(\displaystyle -1 \) мен \(\displaystyle 2{\small } \) арасындағы барлық нүктелер көрсетілген

Яғни, координаттары \(\displaystyle -1 \)-ден артық және \(\displaystyle 2{\small }\)-ден кем барлық нүктелер бейнеленген.
Басқаша айтқанда, бұл \(\displaystyle -1<x < 2{\small }\) болатын \(\displaystyle x\) координатасы бар барлық нүктелер. Мұндай жиын келесідей белгіленеді \(\displaystyle (-1{\small ; }\,2){\small . } \)
Осылайша, ізделініп отырған сандық аралық:
\(\displaystyle x \in (-1{\small ; }\,2){\small . } \)
Жауабы: \(\displaystyle x \in (-1{\small ; }\,2){\small . } \)
Суретте \(\displaystyle 3\) қоса алғанда және \(\displaystyle 4{\small } \) қоса алғанда \(\displaystyle 3 \) пен \(\displaystyle 4{\small } \) арасындағы барлық нүктелер көрсетілген
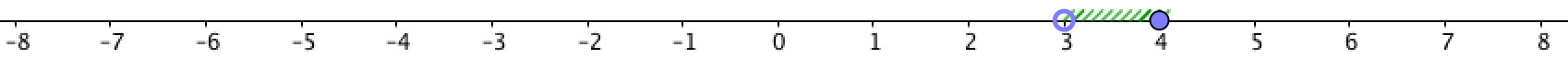
Яғни, координаттары \(\displaystyle 3 \)-тен артық және \(\displaystyle 4{\small }\)-тен кем немесе оған тең барлық нүктелер бейнеленген.
Басқаша айтқанда, бұл \(\displaystyle 3<x \le 4{\small }\) болатын \(\displaystyle x\) координатасы бар барлық нүктелер. Мұндай жиын келесідей белгіленеді \(\displaystyle (3{\small ; }\,4]{\small . } \)
Осылайша, ізделініп отырған сандық аралық:
\(\displaystyle x \in (3{\small ; }\,4]{\small . } \)
Жауабы: \(\displaystyle x \in (3{\small ; }\,4]{\small . } \)
Суретте \(\displaystyle -4\) қосқанда және \(\displaystyle -1{\small } \) қоспағанда \(\displaystyle -4 \) және \(\displaystyle -1{\small } \) арасындағы барлық нүктелер көрсетілген:

Яғни, координаттары \(\displaystyle -4 \) артық немесе оған тең және \(\displaystyle -1{\small }\) кем барлық нүктелер бейнеленген.
Басқаша айтқанда, бұл \(\displaystyle -4\le x <-1{\small }\) болатын \(\displaystyle x\) координатасы бар барлық нүктелер. Мұндай жиын келесідей белгіленеді \(\displaystyle [-4{\small ; }\,-1){\small . } \)
Осылайша, ізделініп отырған сандық аралық:
\(\displaystyle x \in [-4{\small ; }\,-1){\small . } \)
Жауабы: \(\displaystyle x \in [-4{\small ; }\,-1){\small . } \)