Жартылай интервалдар мен жартылай кесінділерге сәйкес келетін нүктелердің геометриялық орнын сызыңыз:
\(\displaystyle (-4;\,-1)\qquad [-1;\ 2] \qquad (3;\,4] \qquad [-1;\,2)\)
\(\displaystyle \color{blue}{(-4;\,-1)}\)
Геометриялық тұрғыдан \(\displaystyle (-4; \,-1)\) интервалы интервалдың ұштары болып табылатын нүктелерді қоспағанда \(\displaystyle -4 \) және \(\displaystyle -1{\small , } \) арасында жатқан барлық нүктелердің жиынын білдіреді.
Осы аралыққа сәйкес келетін нүктелер келесідей бейнеленген:

Анықтама бойынша, \(\displaystyle (-4; \,-1)\) – бұл \(\displaystyle -4\)-тен артық және \(\displaystyle -1{\small }\)-ден кем барлық сандардың жиыны, және, демек, координаталық осьте \(\displaystyle -4 \)-тің оң жағында және \(\displaystyle -1{\small }\)-дің сол жағында орналасқан барлық нүктелердің жиыны.
\(\displaystyle \color{blue}{[-1;\,2]}\)
Геометриялық тұрғыдан \(\displaystyle [-1; \,2]\) кесіндісі кесіндінің ұштары болып табылатын нүктелерді қосқанда \(\displaystyle -1 \) және \(\displaystyle 2{\small } \) арасындағы барлық нүктелердің жиынын білдіреді.
Осы кесіндіге сәйкес келетін нүктелер келесідей бейнеленген:

Анықтама бойынша, \(\displaystyle [-1; \,2]\) – бұл \(\displaystyle -1\)-ден артық немесе оған тең және \(\displaystyle 2{\small }\)-ден кем немесе оған тең барлық сандардың жиыны, және, демек, координаталық осьте \(\displaystyle -1 \) мен \(\displaystyle 2{\small }\) қоса алғанда, \(\displaystyle -1 \) оң жағында және \(\displaystyle 2{\small } \) сол жағында орналасқан барлық нүктелердің жиыны болып табылады.
\(\displaystyle \color{blue}{(3;\,4]}\)
Геометриялық тұрғыдан \(\displaystyle (3; \,4]\) жартылай интервалы жартылай интервалдың ұштары болып табылатын \(\displaystyle 3\) нүктесін қоспағанда және \(\displaystyle 4{\small } \) нүктесін қоса алғанда, \(\displaystyle 3\) пен \(\displaystyle 4{\small } \) арасында жатқан барлық нүктелердің жиынын білдіреді.
Осы жартылай интервалға сәйкес келетін нүктелер келесідей бейнеленген:
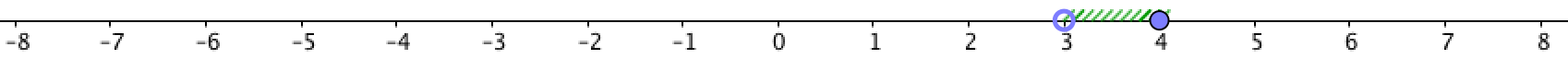
Анықтама бойынша, \(\displaystyle (3; \,4]\) – бұл \(\displaystyle 3\) артық және \(\displaystyle 4{\small }\) кем немесе оған тең барлық сандар жиыны, және, демек, координаталық осьте бұл \(\displaystyle 3\) қоспағанда және\(\displaystyle 4{\small }\) қоса алғанда, \(\displaystyle 3\) оң жағында және \(\displaystyle 4{\small } \) сол жағында орналасқан барлық нүктелер жиыны болып табылады.
\(\displaystyle \color{blue}{[-1;\,2)}\)
Геометриялық тұрғыдан \(\displaystyle [-1; \,2)\) жартылай интервалы жартылай интервалдың ұштары болып табылатын \(\displaystyle -1 \) нүктесін қоса алғанда және \(\displaystyle 2{\small } \) нүктесін қоспағанда, \(\displaystyle -1 \) мен \(\displaystyle 2{\small } \) арасында жатқан барлық нүктелердің жиынын білдіреді.
Осы жартылай интервалға сәйкес келетін нүктелер келесідей бейнеленген:

Анықтама бойынша, \(\displaystyle [-1; \,2)\) – бұл \(\displaystyle -1\)-ден артық немесе оған тең және \(\displaystyle 2{\small }\)-ден кем барлық сандардың жиыны, және, демек, координаталық осьте \(\displaystyle -1 \) қоса алғанда және \(\displaystyle 2{\small }\) қоспағанда оң жағында \(\displaystyle -1 \) және \(\displaystyle 2{\small } \) сол жағында орналасқан барлық нүктелердің жиыны болып табылады.