Теңсіздікті шешіңіз
\(\displaystyle \left( 4^x-5\cdot 2^x \right)^2-20\left( 4^x-5\cdot 2^x \right) -96\leqslant 0{\small .}\)
\(\displaystyle \left( 4^x-5\cdot 2^x \right)^2-20\left( 4^x-5\cdot 2^x \right) -96\leqslant 0{\small .}\)
Теңсіздіктің сол жақ бөлігінде \(\displaystyle 4^x-5\cdot 2^x \) өрнегі және оның квадраты бар.
I. Айнымалыны алмастырып қойайық
\(\displaystyle \color{#336699}{a= 4^x-5\cdot 2^x {\small .}}\)
Квадрат теңсіздікті аламыз:
\(\displaystyle \color{#336699}{a^2-20a-96\leqslant 0{\small .}}\)
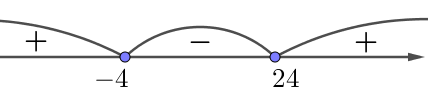
II. Алынған теңсіздікті интервал әдісімен шешейік.
Төмендегіні аламыз:
\(\displaystyle \color{#336699}{-4\leqslant a \leqslant 24{\small .}}\)
III. Ескі айнымалыға оралайық.
Бізде \(\displaystyle {a=4^x-5\cdot 2^x {\small .}}\)
Сонда
\(\displaystyle -4\leqslant 4^x-5\cdot 2^x \leqslant 24{\small .}\)
Теңсіздіктер жүйесін аламыз:
\(\displaystyle \color{#336699}{\left\{\begin{array}{rl}t^2-5t-24& \leqslant \, 0{\small ,}\\t^2-5t+4&\geqslant\, 0{\small .}\\\end{array}\right.}\)
V. Алынған жүйені шешейік.
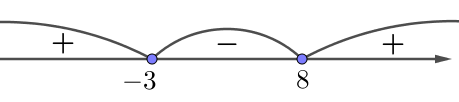
Жүйенің әрбір теңсіздігін шешеміз, содан кейін алынған шешімдер жиынының қиылысын табамыз.
\(\displaystyle -3\leqslant t\leqslant 8\)
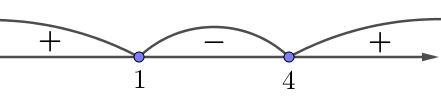
\(\displaystyle -\infty< t\leqslant 1{\small ;} \,\,\,\, 4 \leqslant t < +\infty\)
\(\displaystyle {-3\leqslant t\leqslant 1}{\small;}\) \(\displaystyle {4\leqslant t\leqslant 8{\small.}}\)
VI. Ескі айнымалыға оралайық.
\(\displaystyle x{\small }\) айнымалысына оралайық. Бізде \(\displaystyle t=2^x{\small .}\)
Сонда:
\(\displaystyle \color{Blue}{-3\leqslant 2^x\leqslant 1}\) немесе \(\displaystyle \color{Blue}{4\leqslant 2^x\leqslant 8{\small.}}\)
Әрбір теңсіздікті шешейік.
Қос теңсіздікті теңсіздіктер жүйесі түрінде жазайық:
\(\displaystyle \left\{\begin{array}{rcl}2^x& \geqslant-3,\\[5px]2^x& \leqslant \,1.\\\end{array}\right.\)
Жүйенің әрбір теңсіздігін шешіп, алынған шешімдер жиынының қиылысын табамыз.
- Бірінші теңсіздікті шешейік: \(\displaystyle 2^x \geqslant-3{\small .}\)
\(\displaystyle y=2^x\) көрсеткіштік функциясы тек оң мәндерді қабылдайды, сондықтан \(\displaystyle {2^x \geqslant-3}{\small}\) теңсіздігі \(\displaystyle x{\small }\) айнымалысының кез-келген нақты мәндерінде орындалады
Яғни, бірінші теңсіздіктің шешімі \(\displaystyle (-\infty;+\infty){\small }\) аралығы болып табылады
- Екінші теңсіздікті шешейік: \(\displaystyle 2^x \leqslant 1{\small .}\)
\(\displaystyle 2^x \leqslant 1\Leftrightarrow 2^x \leqslant 2^0{\small .}\)
Дәреженің негізі \(\displaystyle 2>1{\small,}\) болғандықтан, теңсіздіктерге көшкен кезде көрсеткіштерде теңсіздік белгілері өзгермейді.
Төмендегіні аламыз: \(\displaystyle x \leqslant 0{\small. } \)
Яғни, бұл теңсіздіктің шешімі \(\displaystyle (-\infty;0]{\small }\) аралық болып табылады
- Алынған \(\displaystyle (-\infty;+\infty)\) және \(\displaystyle (-\infty;0]\) аралықтарының қиылысы \(\displaystyle (-\infty;0]{\small }\) болып табылады
Қос теңсіздікті теңсіздіктер жүйесі түрінде жазайық:
\(\displaystyle \left\{\begin{array}{rcl}2^x& \geqslant4,\\[5px]2^x& \leqslant \,8.\\\end{array}\right.\Leftrightarrow\left\{\begin{array}{rcl}2^x& \geqslant2^2,\\[5px]2^x& \leqslant \,2^3.\\\end{array}\right.\)
Дәреженің негізі \(\displaystyle 2>1{\small,}\) болғандықтан, теңсіздіктерге көшкен кезде көрсеткіштерде теңсіздік белгілері өзгермейді.
Төмендегіні аламыз:
\(\displaystyle\left\{\begin{array}{rcl}x& \geqslant2,\\[5px]x& \leqslant \,3.\\\end{array}\right.\)
Яғни, берілген қос теңсіздіктің шешімі \(\displaystyle [2;3]{\small }\) аралығы болып табылады
Бастапқы теңсіздіктің шешімі табылған бос аралықтарды біріктіру болып табылады: :
\(\displaystyle \color{Blue}{(-\infty ;0] \cup [2;3]{\small. }} \)
Жауабы: \(\displaystyle x\in (-\infty ;0]{\small } \cup [2;3]{\small. } \)