Теориясы: Максимум және минимум (тригонометриялық функциялар)

\(\displaystyle \begin{aligned}(14x-7\tg x-3{,}5\pi +11)^{\prime}=(14x)^{\prime}-(7\tg x)^{\prime}-(3{,}5\pi)^{\prime}+(11)^{\prime}=14\cdot(x)^{\prime}-7(x)^{\prime}-0+0=\\[5px]=14\cdot1-7\cdot\frac{1}{\cos^2 x}=14-\frac{7}{\cos^2 x}{\small.}\end{aligned}\)

Нөлге тең алым \(\displaystyle \frac{14\cos^2 x-7}{\cos^2 x}\) орнатыңыз:

\(\displaystyle 14\cos^2 x-7=0{\small,}\)

\(\displaystyle 14\cos^2 x=7{\small,}\)

\(\displaystyle \cos^2 x=\frac{1}{2}{\small,}\)  \(\displaystyle \cos x =\sqrt{\frac{1}{2}}\) немесе \(\displaystyle \cos x=-\sqrt{\frac{1}{2}}\) дегенді білдіреді

Иррационал өрнекті \(\displaystyle \sqrt{\frac{1}{2}}\) рационал бөлімі бар бөлшекке келтірейік:

\(\displaystyle \sqrt{\frac{1}{2}}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{\sqrt{2}\cdot{\sqrt{2}}}=\frac{\sqrt{2}}{2}{\small.}\)

\(\displaystyle \cos x = \frac{\sqrt{2}}{2}\) және \(\displaystyle \cos x = -\frac{\sqrt{2}}{2}{\small}\) теңдеулерін аламыз.

Осы теңдеулерді шешейік.

Косинус мәндері осьте \(\displaystyle \rm OX{\small}\) жататындықтан, біз тригонометриялық шеңберді \(\displaystyle x=\frac{\sqrt{2}}{2}\) және \(\displaystyle x=-\frac{\sqrt{2}}{2}{\small}\) түзулерімен қиылысамыз.

Біз шешімдердің төрт жиынтығын аламыз:

\(\displaystyle x_1=\frac{\pi}{4}+2\pi n_1{\small,}\) \(\displaystyle x_2=\frac{3\pi}{4}+2\pi n_2{\small,}\) \(\displaystyle x_3=-\frac{\pi}{4}+2\pi n_3{\small,}\) \(\displaystyle x_4=-\frac{3\pi}{4}+2\pi n_4{\small,}\)  мұндағы\(\displaystyle n_1{\small,}\,n_2{\small,}\,n_3{\small,}\,n_4 \in \mathbb{Z}\)

Бөлгішті \(\displaystyle \frac{14\cos^2 x-7}{\cos^2 x}\) нөлге қойыңыз:

\(\displaystyle \cos^2 x=0{\small,}\) значит, \(\displaystyle \cos x =0{\small.}\)

Элементар тригонометриялық теңдеуді шешейік \(\displaystyle \cos x = 0{\small.}\)

Косинустың мәндері осьте \(\displaystyle \rm OX{\small}\) жататындықтан, біз түзу \(\displaystyle x=0\) мен тригонометриялық шеңберді қиып өтеміз.

Біз шешімдердің екі жиынтығын аламыз:

\(\displaystyle x_3=\frac{\pi}{2}+2\pi k{\small,}\,\, k \in \mathbb{Z}\)	\(\displaystyle x_4=-\frac{\pi}{2}+2\pi l{\small,}\,\, l \in \mathbb{Z}\)

Тригонометриялық шеңберді тұрғызайық. Онда алым мен бөлгіштің түбірлеріне сәйкес \(\displaystyle f^{\prime}(x){\small}\) нүктелерді белгілейміз

Бірлік шеңберіне \(\displaystyle \left[-\frac{\pi}{3};\frac{\pi }{3}\right]{\small}\) кесіндіні белгілеңіз, біз аламыз:

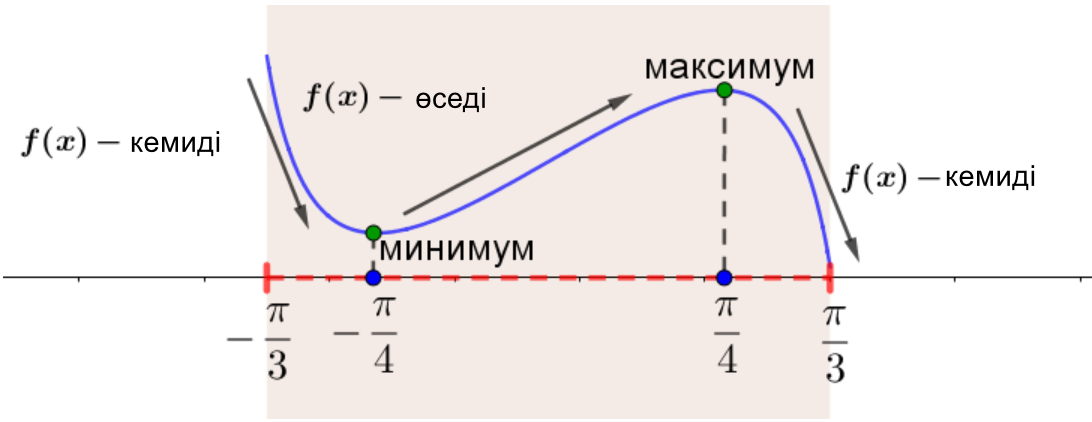
Демек, \(\displaystyle \left[-\frac{\pi}{3};\frac{\pi }{3}\right]\) кесіндісінде екі түбір  \(\displaystyle x=\frac{\pi}{4}\) және \(\displaystyle x=-\frac{\pi}{4}{\small}\) болады.

Функцияның таңбасын \(\displaystyle f^{\prime}(x)=\frac{14\cos^2 x-7}{\cos^2 x}\) аралықтардың әрқайсысында анықтаңыз:

\(\displaystyle \color{green}{\left(-\frac{\pi}{2};\,-\frac{\pi}{4}\right)}{\small,}\) \(\displaystyle \color{Purple}{\left(-\frac{\pi}{4};\,\frac{\pi}{4}\right)}{\small,}\) \(\displaystyle \color{blue}{\left(\frac{\pi}{4};\, \frac{\pi}{2}\right)}{\small.}\)

Ол үшін интервалдардың әрқайсысынан нүктені таңдаймыз және осы нүктедегі функцияның таңбасын анықтаймыз. Аламыз:

• \(\displaystyle \color{green}{x=-\frac{\pi}{3} \in \left(-\frac{\pi}{2};\,-\frac{\pi}{4}\right)}\) белгісі үшін \(\displaystyle f^{\prime}\left(\color{green}{-\frac{\pi}{3}}\right)=\frac{14\cos^2 \left(-\frac{\pi}{3}\right)-7}{\cos^2 \left(-\frac{\pi}{3}\right)}=\frac{14\cos^2 \left(\frac{\pi}{3}\right)-7}{\cos^2 \left(\frac{\pi}{3}\right)}=\frac{14\cdot\frac{1}{4}-7}{\frac{1}{4}}=-14\color{red}{<}0{\small ;}\)
• \(\displaystyle \color{Purple}{x=0 \in \left(-\frac{\pi}{4};\,\frac{\pi}{4}\right)}\) белгісі үшін \(\displaystyle f^{\prime}(\color{Purple}{0})=\frac{14\cos^2 0-7}{\cos^2 0}=\frac{14\cdot1-7}{1}=7\color{red}{>}0{\small;}\)
• \(\displaystyle \color{blue}{x=\frac{\pi}{3} \in{\left(\frac{\pi}{4};\, \frac{\pi}{2}\right)}}\) белгісі үшін \(\displaystyle f^{\prime}\left(\color{blue}{\frac{\pi}{3}}\right)=\frac{14\cos^2-7 \left(\frac{\pi}{3}\right)}{\cos^2 \left(\frac{\pi}{3}\right)}=\frac{14\cdot\frac{1}{4}-7}{\frac{1}{4}}=-14\color{red}{<}0{\small .}\)

білдіреді,

• \(\displaystyle \color{Purple}{\left(-\frac{\pi}{4};\,\frac{\pi}{4}\right)}\) функциясында  \(\displaystyle f^{\prime}(x)>0{\small,}\)
•  интервалдар бойынша \(\displaystyle \color{green}{\left(-\frac{\pi}{2};\,-\frac{\pi}{4}\right)}\) және \(\displaystyle \color{blue}{\left(\frac{\pi}{4};\, \frac{\pi}{2}\right)}\) функциясы \(\displaystyle f^{\prime}(x)<0{\small.}\)