\ \(\displaystyle f(x)=x^3+3x^2-9x-5\) кесіндісінде \(\displaystyle \left[-10;\, 10\right]{\small}\) функцияның ең кіші мәнін табыңыз.
1) \(\displaystyle f(x)=x^3+3x^2-9x-5{\small}\) функциясының туындысын табыңыз.
2) \ \(\displaystyle f^{\prime}(x)=0{\small}\) болатын нүктелерді табайық.
\(\displaystyle f^{\prime}(x)=3x^2+6x-9{\small}\) болғандықтан, ол үшін квадрат теңдеуді шешу керек.
\(\displaystyle 3x^2+6x-9=0{\small.}\)
3) Туындының түбірлерін нақты түзуде белгілейміз, сонымен қатар оның пайда болған интервалдардағы белгілерін анықтаймыз.
- \(\displaystyle \color{green}{(-\infty;\,-3)}\) және \(\displaystyle \textcolor{Purple}{\left(1;\, +\infty\right)}\) аралықтарында\(\displaystyle f^{\prime}(x)>0{\small,}\)
- \(\displaystyle \textcolor{blue}{\left(-3;\, 1\right)}\) функциясы \(\displaystyle f^{\prime}(x)<0{\small}\) интервалында
Суреттегі туындының белгілерін белгілей отырып, біз аламыз:
4) \(\displaystyle f(x)=x^3+3x^2-9x-5{\small}\) ережені пайдаланып функцияның өсу және кему аралықтарын анықтайық.
Егер кез келген нүкте үшін \(\displaystyle x_0\in(a;\,b)\) туынды \(\displaystyle f'(x_0)\) бар болса және \(\displaystyle f'(x_0)>0{\small}\) болса, онда
\(\displaystyle f(x)\) функциясы бүкіл интервалда \(\displaystyle (a;\,b){\small}\) өсуде ( seаrrow )
Егер кез келген нүкте үшін \(\displaystyle x_0\in(a;\,b)\) туынды \(\displaystyle f'(x_0)\) бар болса және \(\displaystyle f'(x_0)<0{\small}\) болса, онда
\(\displaystyle f(x)\) функциясы бүкіл интервалда \(\displaystyle (a;\,b){\small}\) кемуде( seаrrow )
\(\displaystyle f'(x){\small}\) туындының белгілерін білу \(\displaystyle f(x){\small}\) өсу және кему аралықтарын анықтау
Схемалық \(\displaystyle f(x){\small}\) түрде көрсетіңіз
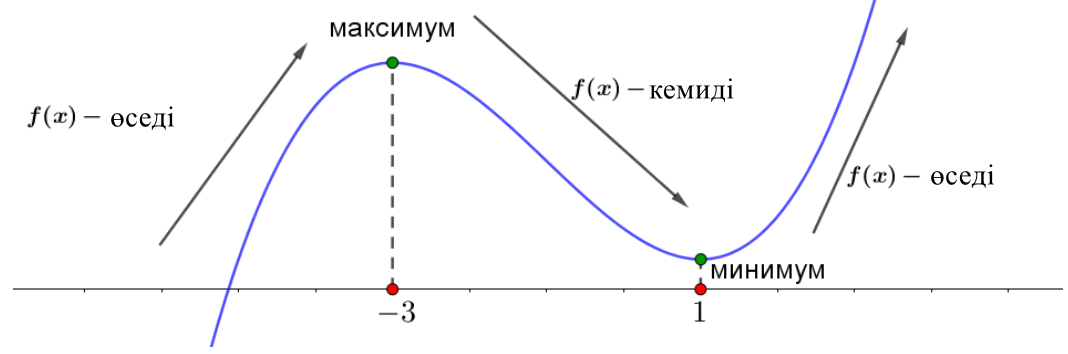
Сонымен, \(\displaystyle x=-3\) - функцияның ең үлкен нүктесі \(\displaystyle f(x)=x^3+3x^2-9x-5{\small.}\)
Ал \(\displaystyle x=1\) –нүктесі ең кіші нүкте болып табылады.
5)\(\displaystyle \left[-10;\,10\right]\) аралық нүктелерінің қайсысында ең кіші мәнге жеткенін анықтайық.
Минималды нүкте \(\displaystyle x=1\) \(\displaystyle \left[-10;\,10\right]{\small}\) интервалына түседі.
Минималды нүктені \(\displaystyle \color{green}{x=1}\) және аралық ұштарын \(\displaystyle \color{blue}{x=-10}\) және \(\displaystyle \textcolor{Purple}{x=10}\) ауыстырыңыз \(\displaystyle f(x)=x^3+3x^2-9x-5{\small:}\)
- \(\displaystyle f(\color{green}{1})=1^3+3\cdot1^2-9\cdot1-5=1+3-9-5=-10{\small,}\)
- \(\displaystyle f(\color{blue}{-10})=(-10)^3+3\cdot(-10)^2-9\cdot(-10)-5=-1000+300+90-5=-615{\small,}\)
- \(\displaystyle f(\textcolor{Purple}{10})=10^3+3\cdot10^2-9\cdot10-5=1000+300-90-5=1205{\small.}\)
Ең кіші мәнге \(\displaystyle \color{green}{x=-10}\) нүктесінде жеткенін және ол \(\displaystyle f(\color{green}{-10})=-615{\small}\) тең екенін көреміз.
Жауабы: \(\displaystyle -615{\small.}\)
Суреттегі \(\displaystyle \left[-10;\,10\right]{\small}\) аралықты белгілеңіз
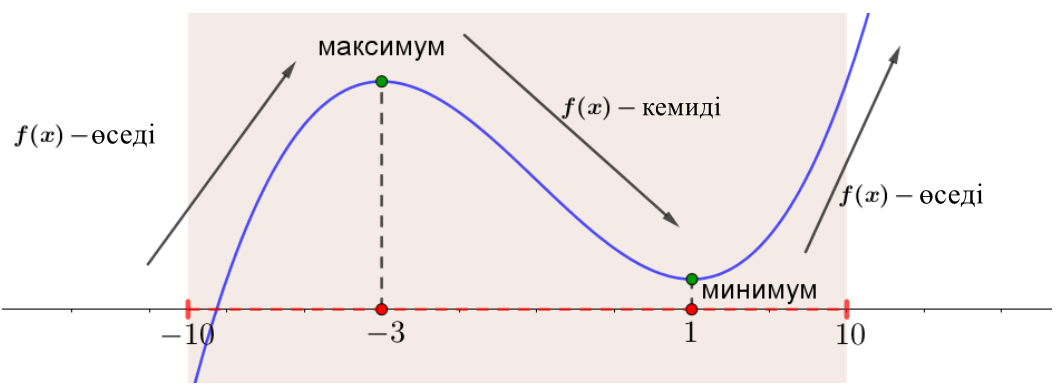
\(\displaystyle \left[-10;\,10\right]\) интервалында \(\displaystyle f(x)\) функциясы өзінің ең кіші мәніне не минималды нүктеде \(\displaystyle x=1{\small}\) немесе сол жақ шетінде \(\displaystyle x=-10{\small}\) жететінін көруге болады.