Теңсіздікті шешіңіз
\(\displaystyle x^2 - 3x -4<0{\small ,}\)
егер сәйкес квадраттық функцияның графигі белгілі болса.
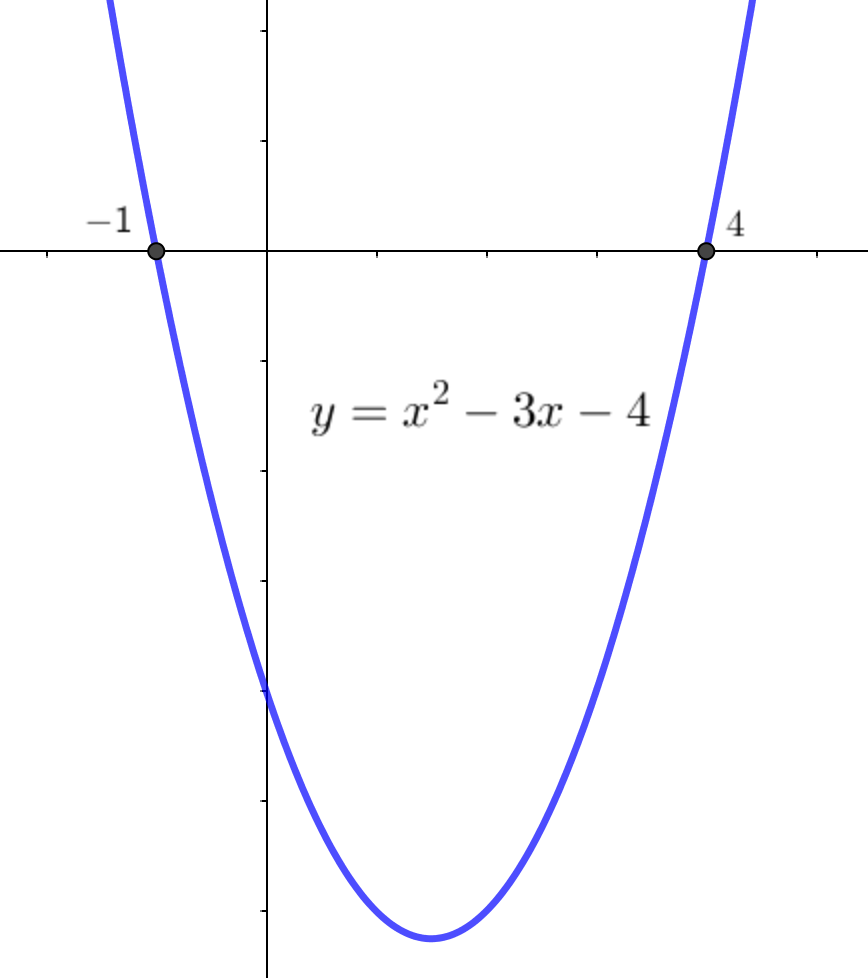
\(\displaystyle x^2 - 3x -4<0\) теңсіздікті шешу үшін \(\displaystyle x^2 - 3x -4 \) мәнін нөлден аз беретін \(\displaystyle x{ \small ,} \) мәндерін табу керек.
\(\displaystyle y=x^2 - 3x -4 \) парабола үшін бұл \(\displaystyle y\) нөлден аз болатын \(\displaystyle x{ \small ,} \) мәндерін табу керек дегенді білдіреді.
Яғни, параболаның тиісті нүктелері \(\displaystyle \rm OX {\small }\) осьтен төмен орналасқан \(\displaystyle x{ \small } \) анықтау керек
\(\displaystyle \rm OX {\small }\) осьтің астында орналасқан парабола нүктелерін қызыл түспен бөлектеңіз
Берілген нүктелердің \(\displaystyle x{ \small } \) координаттарын анықтайық:
Бұл параболаның \(\displaystyle \rm OX {\small }\) осімен қиылысу нүктелерінің арасында жатқан нүктелер екенін аламыз (қиылысу нүктелері жоқ, өйткені оларда \(\displaystyle x^2 - 3x -4=0\)).
Яғни, бұл \(\displaystyle -1\) мен \(\displaystyle 4\)арасындағы барлық нүктелер
Осылайша, теңсіздікті түзу сызықта шешу келесідей:
Түзу сызықта \(\displaystyle x{ \small } \) координаты \(\displaystyle -1\) үлкен және одан \(\displaystyle 4\) кіші барлық нүктелер бейнеленген.
Яғни, бұл барлық нүктелер \(\displaystyle -1<x<4{\small } \) арналған
Мұны аралық ретінде қайта жаза отырып, аламыз:
\(\displaystyle x\in (-1;\, 4){\small .}\)
Жауабы: \(\displaystyle x\in (-1;\, 4){\small .}\)