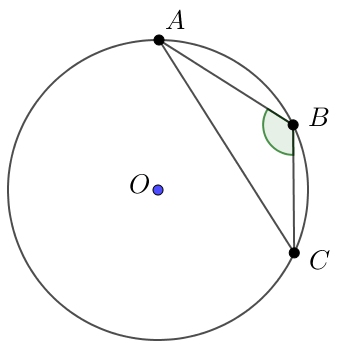
\(\displaystyle ABC\) үшбұрышы центрі \(\displaystyle O \small\) болатын шеңберге іштей сызылған, бұл ретте \(\displaystyle AC=6 \small,\) \(\displaystyle \sin B=0{,}6 \)(суретті қараңыз.). Шеңбердің диаметрін табыңыз.
\(\displaystyle AD \small \) диаметрін құрайық
\(\displaystyle ABCD\) төртбұрышы шеңберге іштей сызылған.
Іштей сызылған төртбұрыш қасиеті бойынша
\(\displaystyle \angle ABC+\angle ADC=180^{\circ} \small.\)
Сонда
\(\displaystyle \angle ADC=180^{\circ}-\angle ABC \small.\)
Келтіру формуласы бойынша
\(\displaystyle \sin \angle D=\sin (\angle ADC)=\sin (180^{\circ}-\angle ABC)=\sin (\angle ABC)=\sin \angle B=0{,}6 \small.\)
Диаметрге тірелетін іштей сызылған бұрыш тік болғандықтан \(\displaystyle ADC\) үшбұрышы тікбұрышты болады.
Тікбұрышты \(\displaystyle ADC\) үшбұрышында
\(\displaystyle \sin \angle D=\frac{AC}{AD} \small.\)
Сонда
\(\displaystyle AD=\frac{AC}{\sin \angle D}=\frac{6}{0{,}6}=10 \small.\)
Демек, шеңбердің диаметрі \(\displaystyle 10 \small\) тең.
Жауабы: \(\displaystyle 10 {\small .}\)
\(\displaystyle ABC \small,\) доғал бұрышының \(\displaystyle AC\) қабырғасы мен сырттай сызылған шеңбердің диаметрі арасындағы байланысты зерттеу келесі қатынасты алуға мүмкіндік береді:
Үшбұрыштың қабырғасы, қарама-қарсы бұрыш және сырттай сызылған шеңбердің радиусы арасындағы байланыс
Егер \(\displaystyle ABC\) үшбұрышында \(\displaystyle ABC\) бұрышы доғал болса, онда
\(\displaystyle \frac{AC}{\sin \angle B}=2R \small,\)
мұндағы \(\displaystyle R\) – сырттай сызылған шеңбердің радиусы.