Диагональ и сторона ромба относятся как \(\displaystyle 6 : 5 \small.\) Другая диагональ ромба равна \(\displaystyle 8 \small.\) Найдите сторону ромба.


Пусть \(\displaystyle BD:AB=6:5 \small,\) \(\displaystyle AC=8 \small.\) Равенство \(\displaystyle BD:AB=6:5\) означает, что если мы разделим отрезок \(\displaystyle BD\) на \(\displaystyle 6\) равных частей, то отрезок \(\displaystyle AB\) можно разделить на \(\displaystyle 5\) таких же частей.

Обозначим через \(\displaystyle x\) длину одной части. Тогда \(\displaystyle BD=6x \small,\) а \(\displaystyle AB=5x \small.\)
Пусть \(\displaystyle O\) – точка пересечения диагоналей ромба \(\displaystyle ABCD \small.\)

По свойству параллелограмма диагонали точкой пересечения делятся пополам. Значит,
\(\displaystyle AO=OC=4\) и \(\displaystyle BO=OD={3x} \small.\)
По свойству ромба диагонали перпендикулярны.
Значит, угол \(\displaystyle AOB\) – прямой.
В прямоугольном треугольнике \(\displaystyle AOB\) по теореме Пифагора
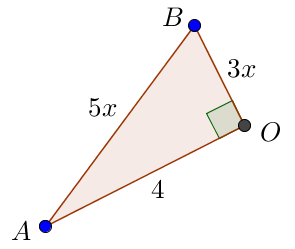
\(\displaystyle AB^2=AO^2+OB^2 \small.\)
Тогда
\(\displaystyle (5x)^2=(4)^2+({3x})^2 \small,\)
\(\displaystyle 25x^2=16+{9x^2} \small,\)
\(\displaystyle {25x^2-9x^2}=16 \small,\)
\(\displaystyle {16x^2}={16} \small,\)
\(\displaystyle {x^2}={1} \small.\)
Поскольку длина отрезка положительна, то
\(\displaystyle x=1 \small.\)
Тогда
\(\displaystyle AB=5x=5 \small.\)
Ответ: \(\displaystyle 5 {\small .}\)