Ромбтың диагоналы мен қабырғасы өзара байланысты \(\displaystyle 6 : 5 \small.\) Ромбтың басқа диагоналы \(\displaystyle 8 \small.\) Ромбтың қабырғасын табыңыз.


\(\displaystyle BD:AB=6:5 \small,\) \(\displaystyle AC=8 \small.\) Теңдігі \(\displaystyle BD:AB=6:5\) егер \(\displaystyle BD\) кесіндісін \(\displaystyle 6\) тең бөлікке бөлсек, онда \(\displaystyle AB\) кесіндісін алайық \(\displaystyle 5\) бірдей бөліктерге бөлуге болады.

Бір бөліктің ұзындығын \(\displaystyle x\) арқылы белгілеңіз. Сонда \(\displaystyle BD=6x \small,\) ал \(\displaystyle AB=5x \small.\)
\(\displaystyle O\) – ромбтың \(\displaystyle ABCD \small\) диагональдарының қиылысу нүктесі болсын

Параллелограмның қасиетіне сәйкес диагональдар қиылысу нүктесіне қарай екіге бөлінеді. Демек,
\(\displaystyle AO=OC=4\) және \(\displaystyle BO=OD={3x} \small.\)
Ромбтың қасиеті бойынша диагональдары перпендикуляр.
Сонымен бұрыш \(\displaystyle AOB\) – тік бұрыш болады.
Пифагор теоремасы бойынша \(\displaystyle AOB\) тікбұрышты үшбұрышта
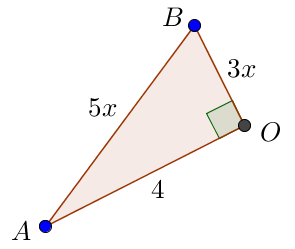
\(\displaystyle AB^2=AO^2+OB^2 \small.\)
Содан кейін
\(\displaystyle (5x)^2=(4)^2+({3x})^2 \small,\)
\(\displaystyle 25x^2=16+{9x^2} \small,\)
\(\displaystyle {25x^2-9x^2}=16 \small,\)
\(\displaystyle {16x^2}={16} \small,\)
\(\displaystyle {x^2}={1} \small.\)
Қиманың ұзындығы оң болғандықтан, онда
\(\displaystyle x=1 \small.\)
Содан кейін
\(\displaystyle AB=5x=5 \small.\)
Жауабы: \(\displaystyle 5 {\small .}\)