Биіктігі \(\displaystyle \sqrt{3} \small\) және сүйір бұрышы \(\displaystyle 60^\circ \small\) болатын ромбтың қабырғасын табыңыз.
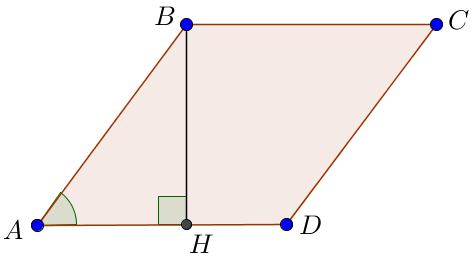

Тік бұрышты үшбұрыштың \(\displaystyle ABH{\small }\) ромбының \(\displaystyle AB\) қабырғасын табыңыз
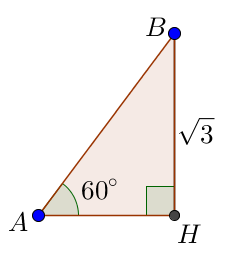
\(\displaystyle BH\) – сүйір бұрышқа қарама-қарсы катет. \(\displaystyle A \small,\) \(\displaystyle AB\) – \(\displaystyle ABH{\small }\) тікбұрышты үшбұрыштың гипотенузасы Сонда
\(\displaystyle AB=\frac{BH}{\sin A} = \frac{\sqrt{3}}{\sin 60^{\circ}}=\frac{\phantom{1}\sqrt{3}\phantom{1}}{\frac{\sqrt{3}}{2}}=\frac{2\sqrt{3}}{{\sqrt{3}}}={2} \small.\)
Жауабы: \(\displaystyle 2{\small .}\)