Адам \(\displaystyle 4{,}2\) м биіктікте орналасқан шам ілулі тұрған бағанадан \(\displaystyle 6\) м қашықтықта тұрады. Адамның көлеңкесі \(\displaystyle 1{,}8\) м тең. Адамның бойын табыңыз (метрмен) ?

\(\displaystyle \red{ h}\) – адамның бойы болсын.
Есепте ұсынылған құрылымды \(\displaystyle \triangle ABC \) және \(\displaystyle \triangle DBH\small, \) тікбұрышты үшбұрыштар түрінде бейнелейік, ондағы:
- \(\displaystyle D\) нүктесі \(\displaystyle AB\small, \) \(\displaystyle H\) нүктесі \(\displaystyle BC\small \) жатыр
- \(\displaystyle \angle ACB =90^{\circ} \small, \) \(\displaystyle \angle DHB =90^{\circ} \small, \)
- \(\displaystyle CH=4{,}2 \small, \) \(\displaystyle BH=1{,}8 \small, \) \(\displaystyle AC=6 \small, \) \(\displaystyle DH=\red{h} \small. \)
\(\displaystyle \triangle ABC \) және \(\displaystyle \triangle DBH\small \) үшбұрыштарын қарастырайық
Себебі \(\displaystyle \angle ACB =\angle DHB =90^{\circ} \) және \(\displaystyle \angle B \) – ортақ,
онда \(\displaystyle \triangle ABC \) және \(\displaystyle \triangle DBH\) үшбұрыштары екі бұрышқа ұқсас.
Сонда \(\displaystyle \frac{AC}{DH}=\frac{BC}{BH} \small.\) \(\displaystyle DH\small \) өрнектейік \(\displaystyle DH= \frac{AC \cdot BH}{BC} \small, \\ \) \(\displaystyle \red{h}= \frac{6 \cdot 1{,}8}{BC} \small.\) \(\displaystyle BC \small \) табамыз \(\displaystyle BC=CH+BH \small,\) \(\displaystyle BC=4{,}2+1{,}8=6 \small.\) Төмендегіні аламыз \(\displaystyle \red{h}= \frac{6 \cdot 1{,}8}{6}=1{,}8 \small.\) | 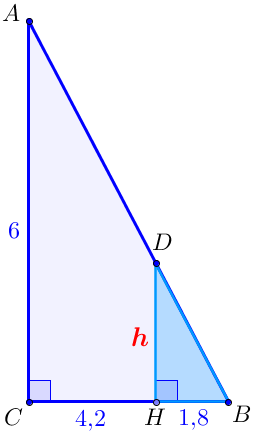 |
Адамның бойы \(\displaystyle 1{,}8\) метрге тең.
Жауабы: \(\displaystyle 1{,}8 \small. \)