Найдите высоту в треугольнике \(\displaystyle ABC{ \small ,}\) проведенную из вершины \(\displaystyle B\) к стороне \(\displaystyle AC{\small .}\)
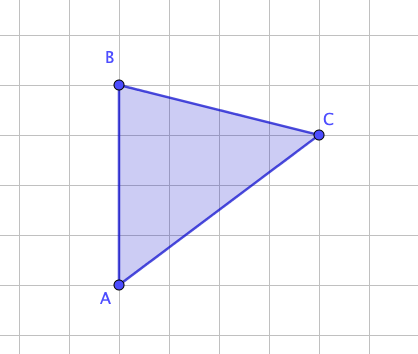
Площадь треугольника равна половине произведения основания на высоту.
Найдем площадь данного треугольника двумя способами.
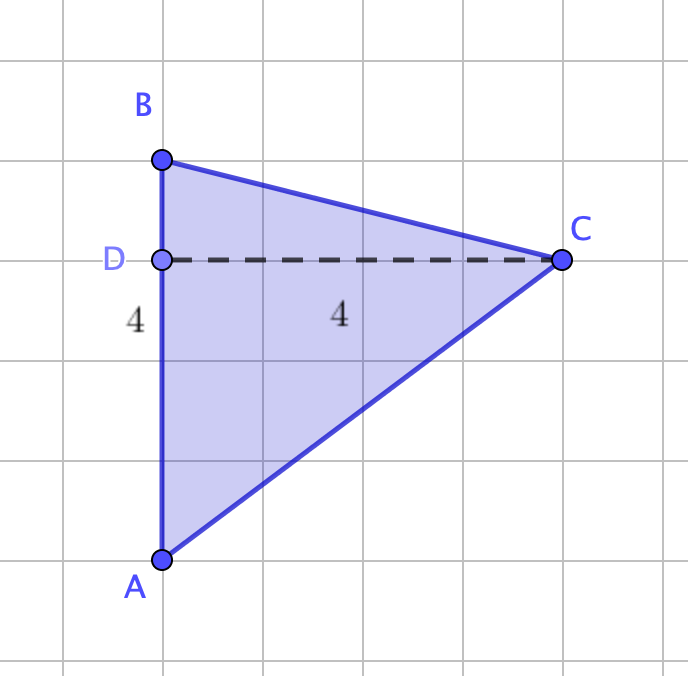
\(\displaystyle S_{ABC}=\frac{1}{2}\cdot BA\cdot CD{ \small ,}\)
\(\displaystyle S_{ABC}=\frac{1}{2}\cdot 4\cdot 4{ \small ,}\)
\(\displaystyle S_{ABC}=8{\small .}\)
С другой стороны, найдем длину стороны \(\displaystyle AC\) по теореме Пифагора:
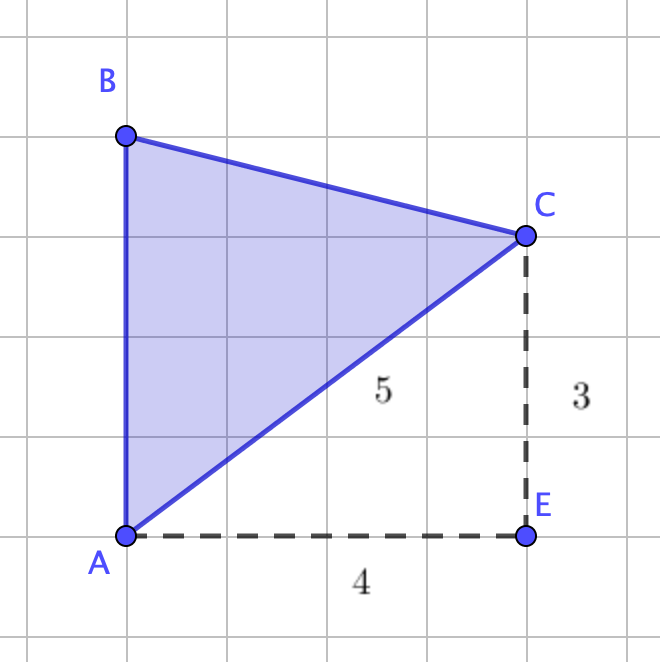
\(\displaystyle AC^2=3^2+4^2{ \small ,}\)
\(\displaystyle AC^2=25{ \small ,}\)
\(\displaystyle AC=5{\small .}\)
Площадь треугольника равна
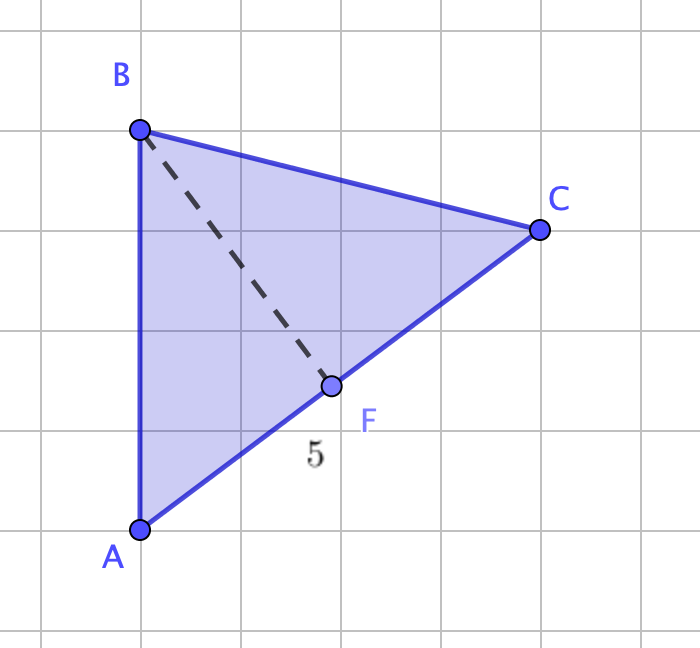
\(\displaystyle S_{ABC}=\frac{1}{2}\cdot BF\cdot CA{ \small ,}\)
\(\displaystyle S_{ABC}=\frac{1}{2}\cdot BF\cdot 5\) и \(\displaystyle S_{ABC}=8{\small .}\)
Тогда
\(\displaystyle 8=\frac{1}{2}\cdot BF\cdot 5{ \small ,}\)
\(\displaystyle BF=\frac{16}{5}{\small .}\)
Ответ:\(\displaystyle \frac{16}{5}{\small .}\)