\(\displaystyle B\) төбесінен \(\displaystyle AC \) қабырғасына жүргізілген \(\displaystyle ABC\) үшбұрышындағы биіктікті табыңыз
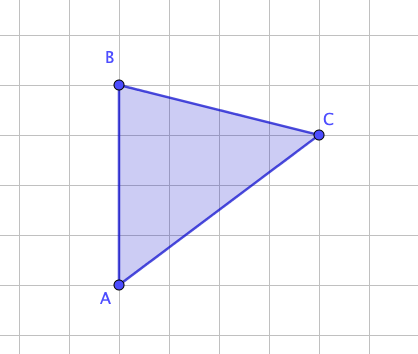
Үшбұрыштың ауданы табанның биіктікке көбейтіндісінің жартысына тең.
Осы үшбұрыштың ауданын екі жолмен табайық.
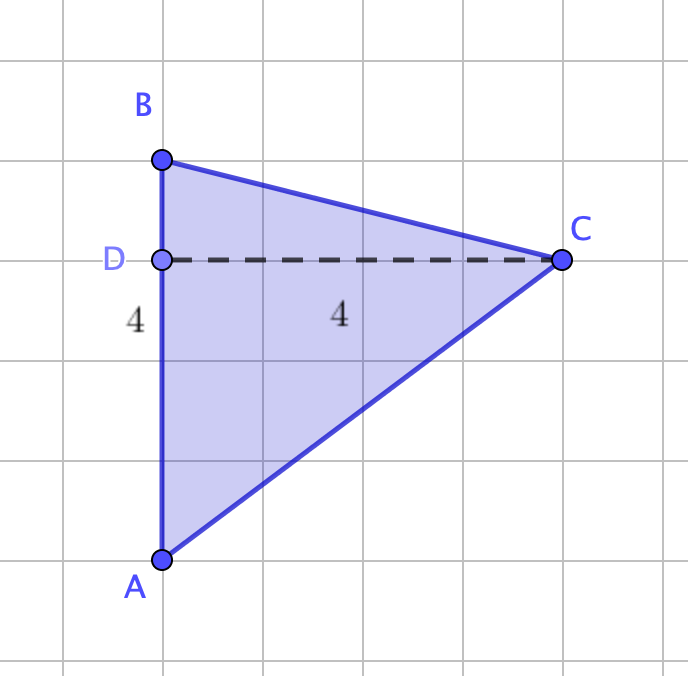
\(\displaystyle S_{ABC}=\frac{1}{2}\cdot BA\cdot CD{ \small ,}\)
\(\displaystyle S_{ABC}=\frac{1}{2}\cdot 4\cdot 4{ \small ,}\)
\(\displaystyle S_{ABC}=8{\small .}\)
Екінші жағынан, Пифагор теоремасы бойынша \(\displaystyle AC\) қабырғасының ұзындығын табамыз:
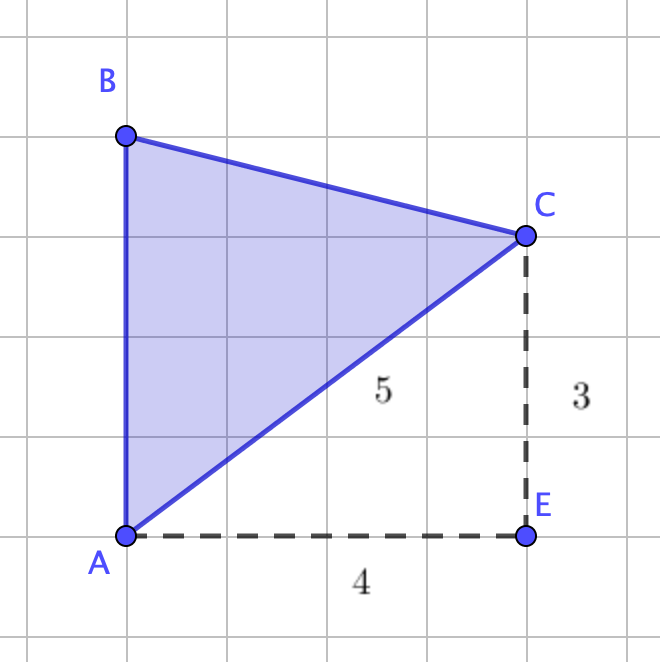
\(\displaystyle AC^2=3^2+4^2{ \small ,}\)
\(\displaystyle AC^2=25{ \small ,}\)
\(\displaystyle AC=5{\small .}\)
Үшбұрыштың ауданы
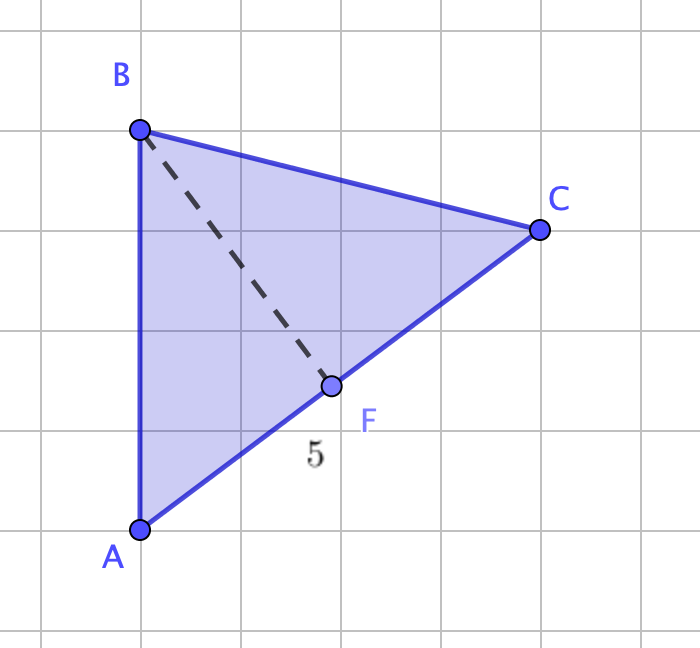
\(\displaystyle S_{ABC}=\frac{1}{2}\cdot BF\cdot CA{ \small ,}\)
\(\displaystyle S_{ABC}=\frac{1}{2}\cdot BF\cdot 5\) және \(\displaystyle S_{ABC}=8{\small .}\)
Онда
\(\displaystyle 8=\frac{1}{2}\cdot BF\cdot 5{ \small ,}\)
\(\displaystyle BF=\frac{16}{5}{\small .}\)
Жауабы:\(\displaystyle \frac{16}{5}{\small .}\)