Егер бірлік квадраттарының торы қолданылса, үшбұрыштың периметрін табыңыз.
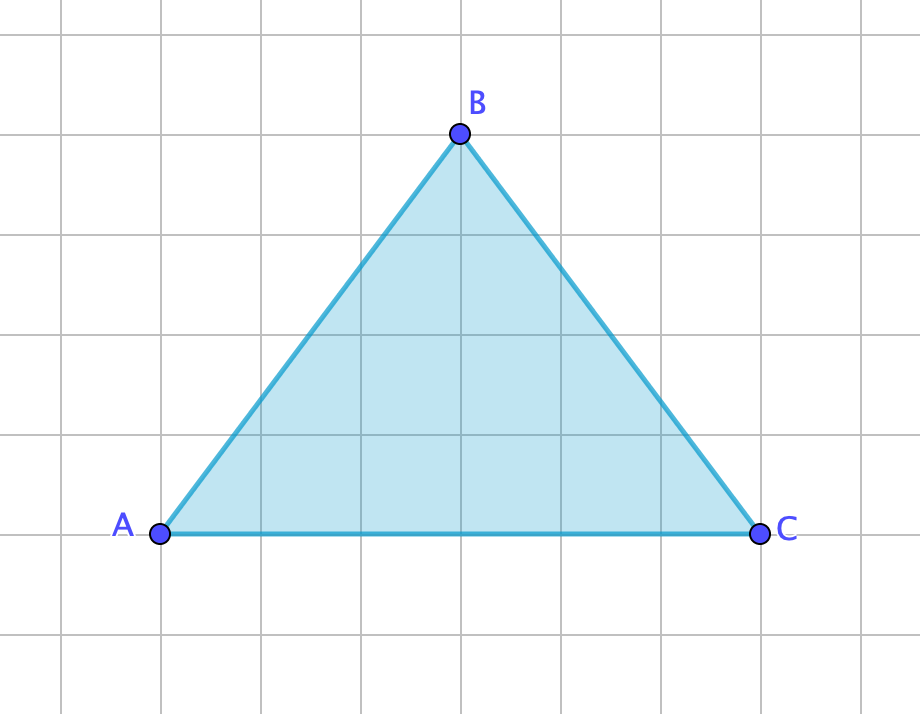
Биіктікті \(\displaystyle AB{\small }\) табанына қарай түсірейік. Катеттері \(\displaystyle 3\) және \(\displaystyle 4{\small }\) болатын екі тікбұрышты \(\displaystyle ABD\) және \(\displaystyle BDC\) үшбұрыштарын аламыз
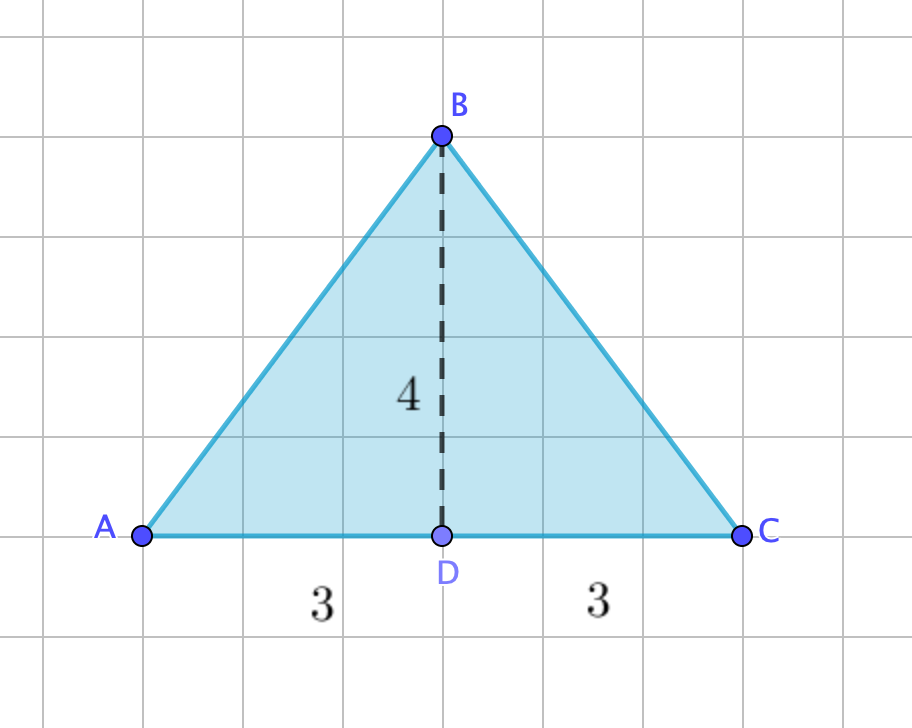
Сонда Пифагор теоремасы бойынша \(\displaystyle AB\) және \(\displaystyle BC\) гипотенузалары төмендегілерге тең
\(\displaystyle AB=\sqrt{3^2+4^2}{ \small ,}\)
\(\displaystyle AB=\sqrt{25}{ \small ,}\)
\(\displaystyle AB=5\)
және
\(\displaystyle BC=\sqrt{3^2+4^2}{ \small ,}\)
\(\displaystyle BC=\sqrt{25}{ \small ,}\)
\(\displaystyle BC=5{\small .}\)
Осылайша, бізге үшбұрыштың барлық қабырғаларының ұзындықтары белгілі

Периметр
\(\displaystyle AB+BC+CA=5+5+6=16{\small }\) тең
Жауабы: \(\displaystyle 16{\small .}\)