Суретте \(\displaystyle y = F(x)\) кейбір функцияның түрлендірілген түрлерінің бірі \(\displaystyle f(x)\) графигі көрсетілген және абсцисса осінде он нүкте белгіленген: \(\displaystyle x_1,\, x_2,\, x_3,\, x_4,\, x_5,\, x_6,\, x_7,\, x_8{\small.}\) Осы \(\displaystyle f(x)\) нүктелердің қанша функциясы теріс?
Егер \(\displaystyle F(x)\) – \(\displaystyle f(x){\small}\) түрленген функция болса, онда
\(\displaystyle F^{\prime}(x)=f(x){\small.}\)
Демек, \(\displaystyle f(x)\) – \(\displaystyle F(x){\small}\) бұл туынды және тәуелдік орны бар:
| \(\displaystyle F(x)\) әрекет нүктенің маңында | \(\displaystyle f(x)\) белгі нүктеде |
| егер \(\displaystyle F(x)\) өседі, онда | \(\displaystyle f(x)\ge 0\) |
| егер \(\displaystyle F(x)\) кішірейеді, онда | \(\displaystyle f(x)\le 0\) |
Нүктелер маңындағы \(\displaystyle F(x)\) әрекетті қарастырайық \(\displaystyle x_1,\,x_2,\,x_3,\,x_4,\,x_5,\,x_6,\,x_7,\,x_8{\small:}\)
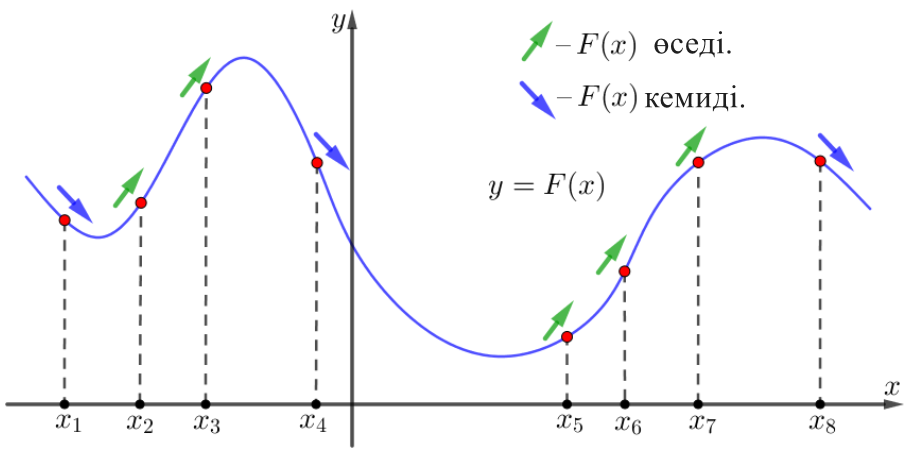
Аламыз:
| Нүктелер | \(\displaystyle F(x)\) әрекет маңында | \(\displaystyle f(x)\) белгі нүктеде |
| \(\displaystyle x_2,\,x_3,\,x_5,\,x_6,\,x_7\) | \(\displaystyle F(x)\) өседі \(\displaystyle \color{#009900}{\nearrow}\) | \(\displaystyle f(x)\ge 0\) |
| \(\displaystyle x_1,\,x_4,\,x_8\) | \(\displaystyle F(x)\) кішірейеді \(\displaystyle \color{#0000FF}{\searrow}\) | \(\displaystyle f(x)\le 0\) |
\\(\displaystyle y=F(x)\) графиктің таңдалған нүктелерінің ешқайсысында жанама\(\displaystyle \rm OX{\small}\) осі параллель емес. Демек, барлық бұл нүктелерде \(\displaystyle F^{\prime}(x)=f(x)\,\cancel{=}\, 0{\small.}\)
Яғни кестеде барлық теңсіздік белгілері қатаң:
| Нүкте | \(\displaystyle f(x)\) белгі нүктеде |
| \(\displaystyle x_2,\,x_3,\,x_5,\,x_6,\,x_7\) | \(\displaystyle f(x)> 0\) |
| \(\displaystyle x_1,\,x_4,\,x_8\) | \(\displaystyle f(x)< 0\) |
Демек, \(\displaystyle f(x)\) үш нүктеде теріс.
Жауабы: \(\displaystyle 3{\small.}\)