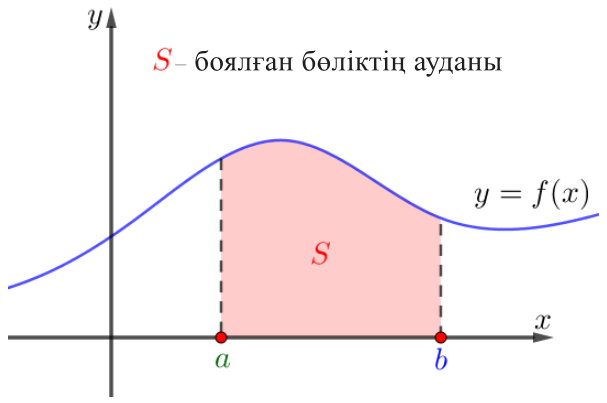
Суретте кейбір \(\displaystyle y=f(x){\small}\) функцияның графигі көрсетілген
Функция \(\displaystyle F(x)=-x^3-27x^2-240x-8\) — \(\displaystyle f(x){\small}\) түрлендірілген функциялардың бірі
Боялған фигураның ауданын табыңыз.
Берілген жағдайда \(\displaystyle F(x){\small}\) түрлендірілген \(\displaystyle f(x){\small}\) содан кейін боялған фигураның ауданын есептеу үшін келесі фактіні қолдануға болады:
Егер \(\displaystyle f(x)\) үздіксіз функция және \(\displaystyle F(x)\) оның түрлендірілген болса, онда графиктің астындағы \(\displaystyle \color{red}{S}\) ауданы (қисық трапеция) формула бойынша есептеледі:
\(\displaystyle \color{red}{S}=F(\color{blue}{b})-F(\color{green}{a}){\small.}\)
[/pr]
Тапсырма жағдайында берілген суретті қарастырайық:
Аламыз:
\(\displaystyle \color{red}{S}=F(\color{blue}{-8})-F(\color{green}{-10}){\small.}\)
\(\displaystyle F(\color{blue}{-8})\) және \(\displaystyle F(\color{green}{-10}){\small}\) есептейміз:
- \(\displaystyle F(\color{blue}{-8})= -(\color{blue}{-8})^3-27\cdot(\color{blue}{-8})^2-240\cdot(\color{blue}{-8})-8=\)\(\displaystyle \kern{10em} =512-1728+1920-8=\color{blue}{696}{\small,}\)
- \(\displaystyle F(\color{green}{-10})= -(\color{green}{-10})^3-27\cdot(\color{green}{-10})^2-240\cdot(\color{green}{-10})-8=\)\(\displaystyle \kern{10em} =1000-2700+2400-8=\color{green}{692}{\small.}\)
Қойып, аламыз:
\(\displaystyle \color{red}{S}=F(\color{blue}{-8})-F(\color{green}{-10})=\color{blue}{696}-\color{green}{692}=4{\small.}\)
Жауабы: \(\displaystyle 4{\small.}\)