Skip to main content

Теориясы: 05 Дөңгелектеу радиусын анықтау

Тапсырма

Үй иесі ағаш пешті таңдады (1-сурет) . Пештің алдыңғы панелінің сызбасы 2 суретте көрсетілген. 

 1- сурет2- сурет

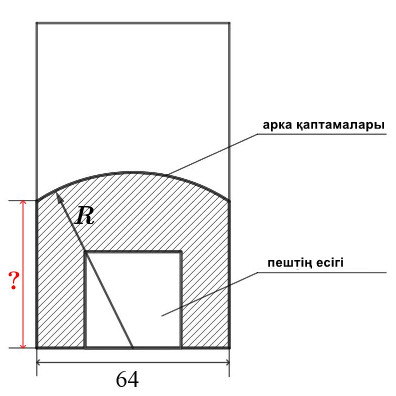
Пеш оттық есігінің айналасында қаптамамен жабдықталған. Қаптаманың жоғарғы бөлігі пештің алдыңғы қабырғасына қаптаманың төменгі бөлігінің ортасымен шеңбер доғасы бойымен дәнекерленген арка түрінде жасалған (2-сурет) .

Арканың дөңгелектеу радиусы \(\displaystyle R\) белгілі және \(\displaystyle 68\) см тең. Қаптаманың ені сантиметрмен суретте көрсетілген. Қаптаманың биіктігін сантиметрмен табыңыз.

Шешім

Сызбаға \(\displaystyle A{\small,}\,B{\small,}\,C{\small,}\,O{\small}\) нүктелерін қосайық 

  Келесіні көреміз

  • \(\displaystyle AC=64\)см.
  • шарт бойынша \(\displaystyle O\)– төменгі бөліктің центрі, яғни,\(\displaystyle AO=OC=\frac{1}{2}AC=\frac{1}{2} \cdot64=32\)см.
  • \(\displaystyle OB\)  \(\displaystyle O\) центрінен қаптаманың доғасына дейінгі арақашықтыққа тең, сондықтан ол да дөңгелектеу радиусы болып табылады: \(\displaystyle OB=R=68\)см.

 

 \(\displaystyle AOB {\small}\) үшбұрышын қарастырайық:

  • \(\displaystyle A\)– бұрышы – тік;
  • катет \(\displaystyle AO=32\)см;
  • гипотенуза \(\displaystyle OB=68\)см.

Пифагор теоремасы бойынша \(\displaystyle AB\) катетін табайық:

\(\displaystyle AB^{\,2}+AO^{\,2}=OB^{\,2}{\small,}\)

\(\displaystyle AB^{\,2}=OB^{\,2}-AO^{\,2}{\small,}\)

\(\displaystyle AB^{\,2}=68^{\,2}-32^{\,2}=3600=60^{\,2}{\small.}\)

 \(\displaystyle AB\)– кесіндінің ұзындығы болғандықтан, онда \(\displaystyle AB>0{\small.}\) 

Яғни, \(\displaystyle AB=60\)см.

Жауабы: \(\displaystyle 60\)