Ойын сүйектері түскен ұпайлардың қосындысы \(\displaystyle 3{\small} \) санынан асып кеткенше лақтырылды. Ол үшін екі лақтыру қажет болғандығының ықтималдығы қандай? Жауабын жүздікке дейін дөңгелектеңіз.
\(\displaystyle A\) – тура екі лақтыру кезінде түскен ұпайлардың қосындысы \(\displaystyle 3{\small} \) санынан асып кетті оқиғасы болсын.
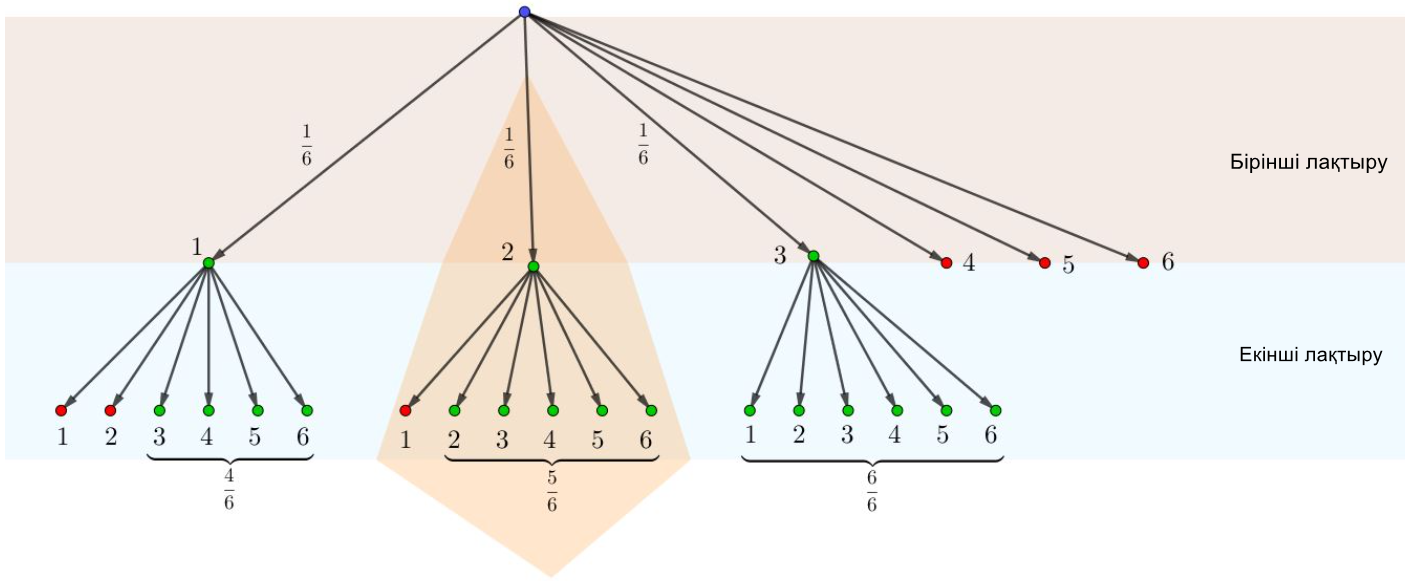
Ойын сүйегінің бірінші лақтырылу нәтижелерін ескере отырып, ықтимал нәтижелердің графигін құруды бастайық.
\(\displaystyle A\) оқиғасының болуы мүмкін болатын нәтижелерді жасыл түспен, ал қызыл түспен - мүмкін емес нәтижелерді белгілейік.
Төмендегіні аламыз:
Келесі оқиғаларды енгізейік:
- \(\displaystyle B_{1}\) – бірінші лақтыруда \(\displaystyle 1{\small }\),
- \(\displaystyle B_{2}\) – бірінші лақтыруда \(\displaystyle 2{\small , }\)
- \(\displaystyle B_{3}\) – бірінші лақтыруда \(\displaystyle 3\) ұпай түсті.
Сонда \(\displaystyle B_{1}{ \small ,}\,B_2\) және \(\displaystyle B_{3}\) оқиғалардың әрқайсысының пайда болу ықтималдығы келесіге тең
\(\displaystyle P(B_{1})=P(B_{2})=P(B_{3})=\frac{1}{6}{\small . }\)
Бұл ықтималдықтарды суретте белгілейік:
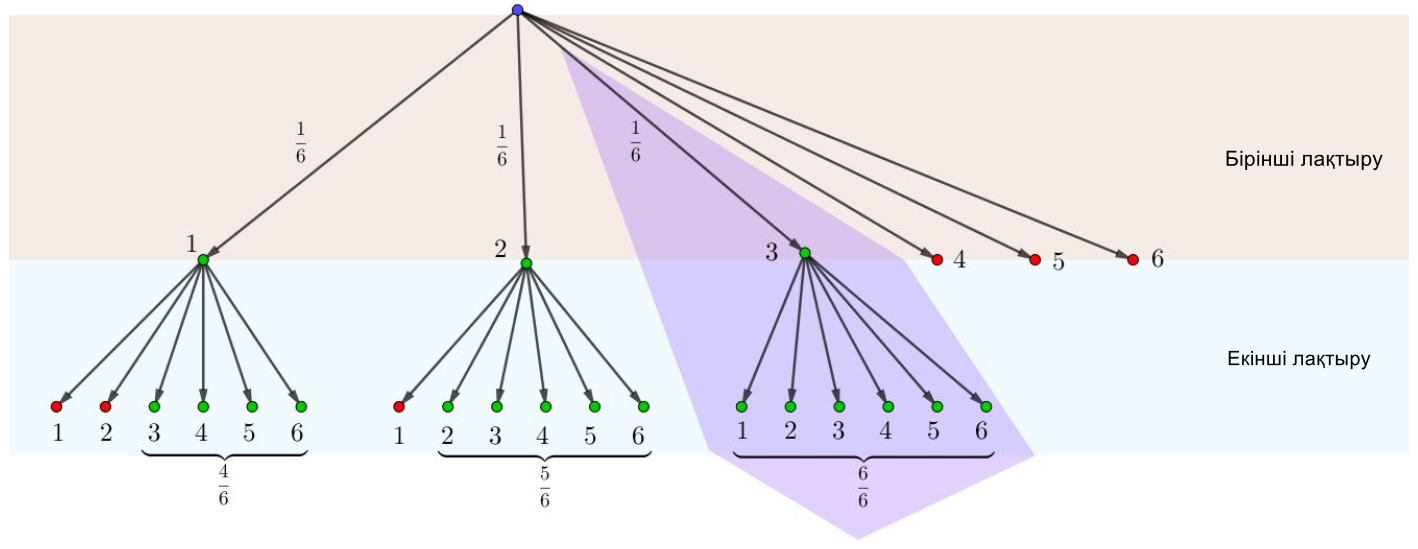
Ықтимал нәтижелердің графигін құруды жалғастырамыз.
Оны ойын сүйегінің екінші лақтырылу нәтижесі бойынша аяқтаймыз.
Тағы да \(\displaystyle A\) оқиғасының болуы мүмкін болатын нәтижелерді жасыл түспен, ал қызыл түспен - мүмкін емес нәтижелерді белгілейік.
Төмендегіні аламыз:
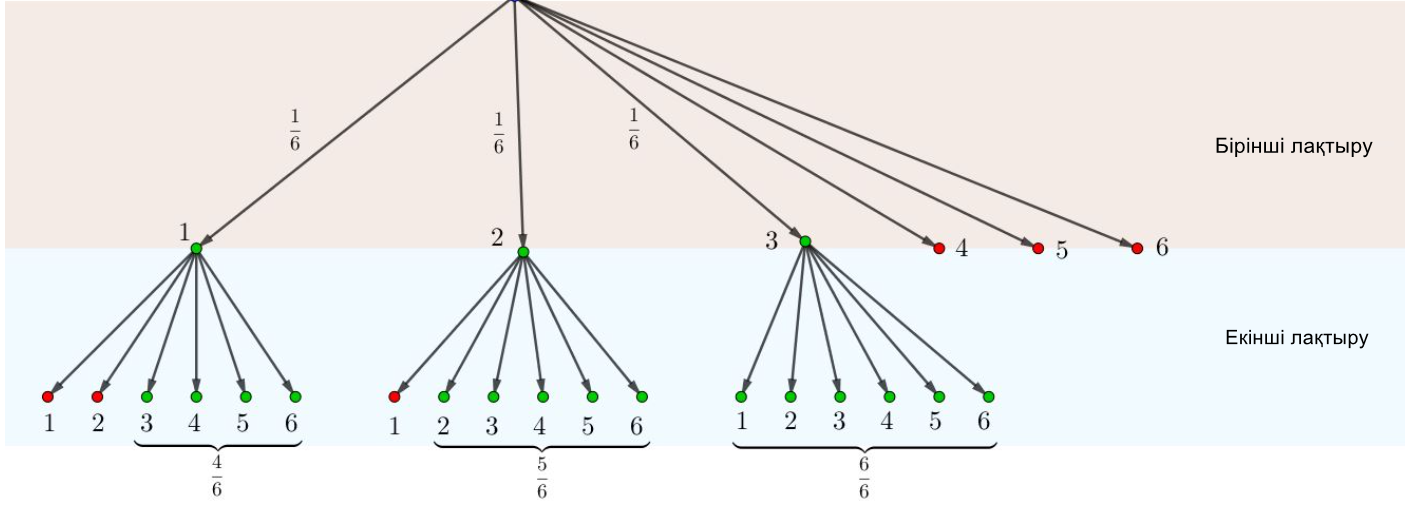
\(\displaystyle P_{B_{1}}(A)\) шартты ықтималдығын табайық – егер \(\displaystyle B_{1}\) оқиғасы болған жағдайда, \(\displaystyle A\) оқиғасының орын алу ықтималдығын.
\(\displaystyle B_{1}\) - бұл бірінші лақтыруда \(\displaystyle 1\) ұпайының түсуі. Демек, \(\displaystyle A\) орын алуы үшін екінші лақтыруда \(\displaystyle 3\), \(\displaystyle 4\), \(\displaystyle 5\) немесе \(\displaystyle 6{\small}\) түсуі керек.
Сонда
\(\displaystyle P_{B_{1}}(A)=\frac{4}{6}{\small . }\)
Сол сияқты,
\(\displaystyle P_{B_{2}}(A)=\frac{5}{6}\) және \(\displaystyle P_{B_{3}}(A)=\frac{6}{6}{\small . }\)
\(\displaystyle A\) және \(\displaystyle B_1{\small}\) оқиғаларының бір уақытта орын алу ықтималдығын есептейміз.
Суретте бұл графиктің бірінші тармағының ықтималдық есебіне ұқсайды:
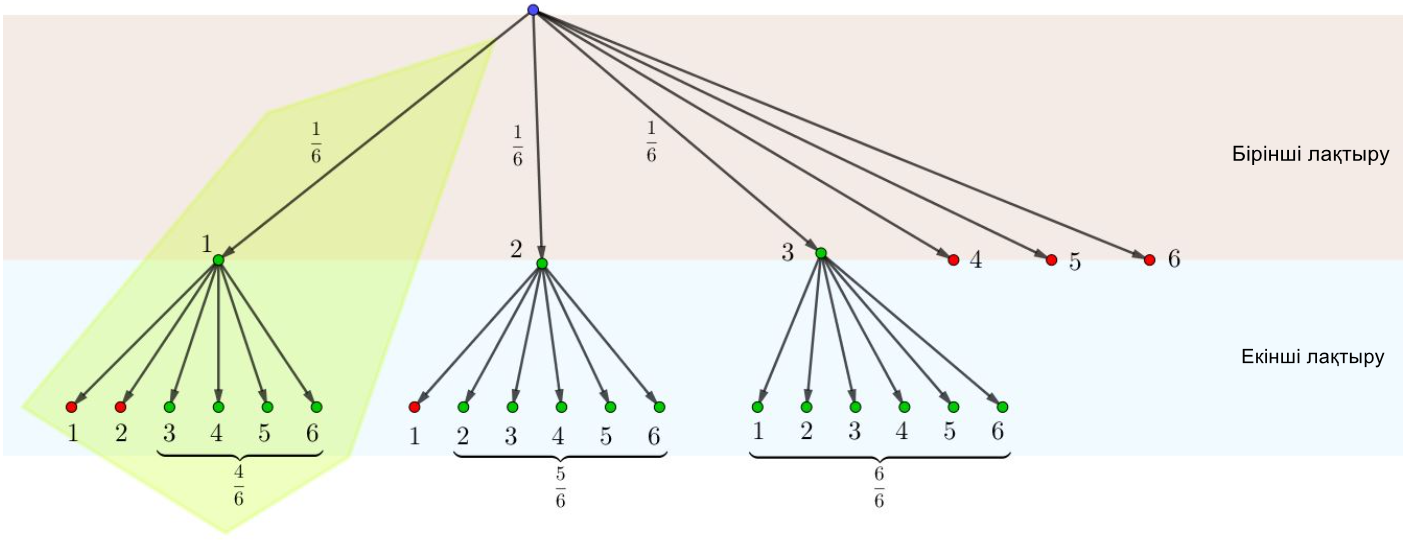
Сонда
\(\displaystyle P(\)бірінші ақтыруда \(\displaystyle 1\) ұпай түсті және қосындысы артық \(\displaystyle 3)=P(B_{1}) \cdot P_{B_{1}}(A)=\frac{1}{6}\cdot\frac{4}{6}=\frac{4}{36}{\small . }\)
Сол сияқты аламыз:
\(\displaystyle А{\small }\) оқиғасының орын алуының жалпы ықтималдығын табу керек.
Ол үшін графигіміздің әрбір тармағы бойынша алынған ықтималдықтарды қосу керек.
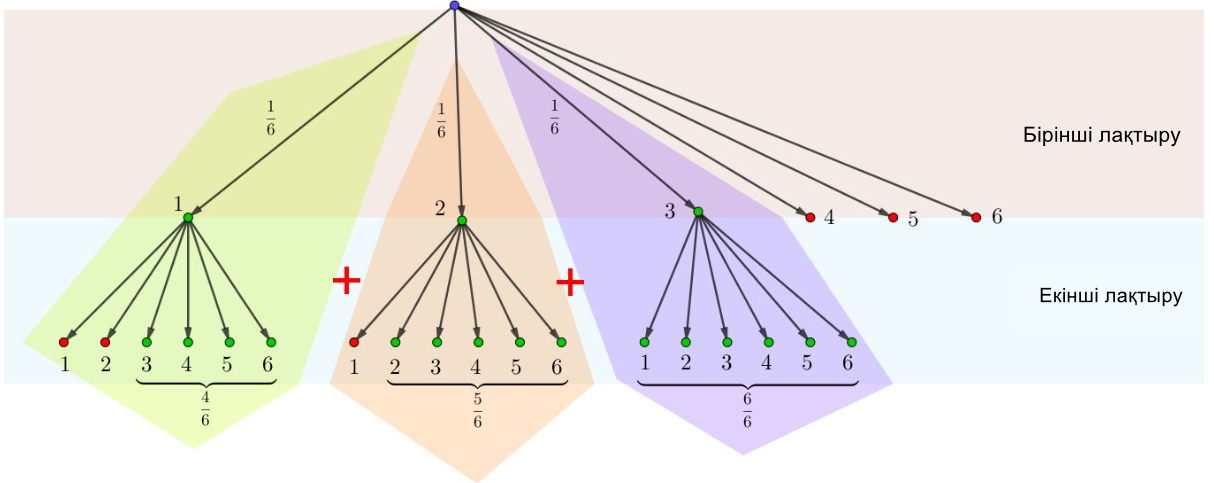
Сонда
\(\displaystyle P(A)=\frac{4}{36}+\frac{5}{36}+\frac{6}{36}=\frac{15}{36}\approx0{,}42{\small . }\)
Жауабы: \(\displaystyle 0{,}42{\small .}\)