Тирдегі атқыш нысанаға тигенше атады. Оның әрбір жеке атыс кезінде \(\displaystyle 0{,}2\) ықтималдықпен нысанаға тиетіні белгілі. Атқыш кем дегенде \(\displaystyle 0{,}84{\small}\) ықтималдықпен нысанаға тиюі үшін оған қанша оқ беру керек?
\(\displaystyle 2^{19}=524\,288,\,2^{20}=1\,048\,576,\,2^{21}=2\,097\,152,\,2^{22}=4\,194\,304,\,2^{23}=8\,388\,608.\)
Жұмсалған патрондар саны атылған ату санымен бірдей екеніне назар аударамыз. Сондықтан алдағы уақытта тек атыстар туралы айтатын боламыз.
Оқиғаларды енгізейік:
- \(\displaystyle A \) – нысанаға тиді,
- \(\displaystyle X\) – бір атқаннан тию,
- \(\displaystyle Y\) – бір атқаннан тимеу.
\(\displaystyle A \) оқиғасы келесі үйлеспейтін оқиғалардан тұрады:
- \(\displaystyle B_{1}\) – бір оқпен нысанаға тигізу,
- \(\displaystyle B_{2}\) – екі оқпен нысанаға тигізу,
- \(\displaystyle B_{3}\) – үш оқпен нысанаға тигізу,
- ...
- \(\displaystyle B_{n}\) – \(\displaystyle n\) оқпен нысанаға тиеді.
Яғни
\(\displaystyle P(A)=P(B_{1})+P(B_{2})+P(B_{3})+...+P(B_{n}){\small . }\)
Демек, \(\displaystyle P(A) \geqslant0{,}84{\small }\) болатын, \(\displaystyle n{\small }\) мәнін табу қажет.
Әрбір ату кезінде екі қарама-қарсы оқиғаның бірі мүмкін – \(\displaystyle X\) немесе \(\displaystyle Y\).
Шарт бойынша \(\displaystyle P(X)=0{,}2{\small .}\) Қарама-қарсы \(\displaystyle Y\) оқиғасының ықтималдығын келесідей табамыз
\(\displaystyle P(Y)=1-P(X)=1-0{,}2=0{,}8{\small .}\)
Нысаға қанша атыстан тигізуге болатынын қарастырайық:
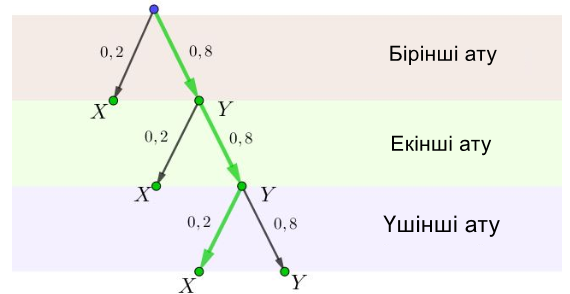
Мүмкін нәтижелердің графигін құруды бастайық. Қолайлы оқиғаны жасыл түспен белгілейік:

Демек,
\(\displaystyle P(B_{1})=P(X)=0{,}2{\small . }\)
Демек, бірінші оқта атқыш мүлт жіберіп, екіншісінде соққы жасады. Сондықтан \(\displaystyle B_{2}\) оқиғасы бірінші атуда \(\displaystyle Y\) оқиғасының және екіншісінде \(\displaystyle X\) оқиғасының бір мезгілде орын алуынан тұрады. Біз мүмкін нәтижелердің графигін құруды жалғастырамыз:
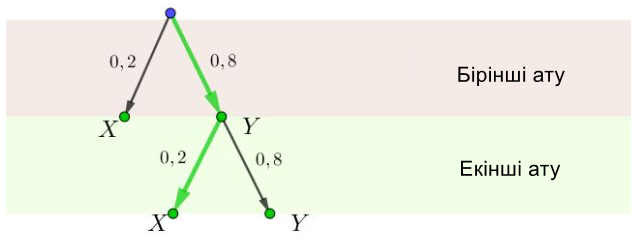
Оқиғалар тәуелсіз болғандықтан, біз мыналарды аламыз:
\(\displaystyle P(B_{2})=P(YX)=P(Y)\cdot P(X)=0{,}8\cdot0{,}2{\small . }\)
Нәтижесінде келесіні аламыз:
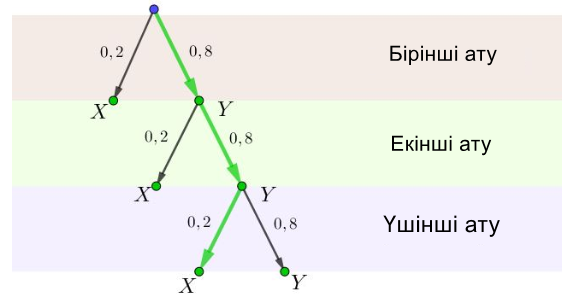
Сонда \(\displaystyle А\) оқиғасының пайда болу ықтималдығы тең болады
\(\displaystyle \begin{aligned}P(A)&=P(B_{1})+P(B_{2})+P(B_{3})+...+P(B_{n})=\\&=0{,}2+0{,}8\cdot0{,}2+0{,}8^2\cdot0{,}2+0{,}8^3\cdot0{,}2+...+0{,}8^{n-1}\cdot 0{,}2=\\&=0{,}2\left(1+0{,}8+0{,}8^2+0{,}8^3+...+0{,}8^{n-1}\right){\small . }\end{aligned}\)
Соңғы өрнектің жақшаларында бірінші мүшесі \(\displaystyle b_{1}=1\) және бөлгіші \(\displaystyle q=0{,}8{\small}\) бар геометриялық прогрессияның мүшелерінің қосындысы \(\displaystyle n\) тұрғанын ескеріңіз.
Осы соманы есептеп көрейік.
Демек,
\(\displaystyle P(A)=0{,2}\cdot\frac{1-0{,}8^n}{0{,}2}=1-0{,}8^n\geqslant0{,}84{\small . }\)
Төмендегі теңсіздікті алдық:
\(\displaystyle 1-0{,}8^n\geqslant0{,}84\)
немесе
\(\displaystyle 0{,}8^n\leqslant0{,}16{\small . }\)
Алынған теңсіздікті түрлендіреміз:
\(\displaystyle \begin{aligned}\left(\frac{8}{10}\right)^n\leqslant\frac{16}{100}{\small , }\\[10px]\left(\frac{2^3}{10}\right)^n\leqslant\frac{2^4}{100}{\small , }\\[10px]\frac{2^{3n}}{10^n}\leqslant\frac{2^4}{10^2}{\small , }\\[10px]2^{3n-4}\leqslant10^{n-2}{\small . }\end{aligned}\)
Соңғы теңсіздікті \(\displaystyle n{\small }\) натурал мәндерін іріктеу арқылы шешейік:
- \(\displaystyle n=1\) – жарамсыз:
\(\displaystyle 2^{3\cdot1-4}\leqslant10^{1-2}{\small , }\)
\(\displaystyle \frac{1}{2}\leqslant \frac{1}{10} \) – дұрыс емес.
- \(\displaystyle n=2\) – жарамсыз:
\(\displaystyle 2^{3\cdot2-4}\leqslant10^{2-2}{\small , }\)
\(\displaystyle 2^2\leqslant10^0{\small , }\)
\(\displaystyle 4\leqslant1 \) – дұрыс емес.
- \(\displaystyle n=3\) – жарамсыз:
\(\displaystyle 2^{3\cdot3-4}\leqslant10^{3-2}{\small , }\)
\(\displaystyle 2^5\leqslant10^2{\small , }\)
\(\displaystyle 32 \leqslant10 \) – дұрыс емес.
- \(\displaystyle n=4\) – жарамсыз:
\(\displaystyle 2^{3\cdot4-4}\leqslant10^{4-2}{\small , }\)
\(\displaystyle 2^{8}\leqslant10^2{\small , }\)
\(\displaystyle 256 \leqslant100 \) – дұрыс емес.
- \(\displaystyle n=5\) – жарамсыз:
\(\displaystyle 2^{3\cdot5-4}\leqslant10^{5-2}{\small , }\)
\(\displaystyle 2^{11}\leqslant10^3{\small , }\)
\(\displaystyle 2048 \leqslant1000 \) – дұрыс емес.
- \(\displaystyle n=6\) – жарамсыз:
\(\displaystyle 2^{3\cdot6-4}\leqslant10^{6-2}{\small , }\)
\(\displaystyle 2^{14}\leqslant10^4{\small , }\)
\(\displaystyle 16384\leqslant10000 \) – дұрыс емес.
- \(\displaystyle n=7\) – жарамсыз:
\(\displaystyle 2^{3\cdot7-4}\leqslant10^{7-2}{\small , }\)
\(\displaystyle 2^{17}\leqslant10^5{\small , }\)
\(\displaystyle 131072 \leqslant100000 \) – дұрыс емес.
- \(\displaystyle n=8\) – жарамсыз:
\(\displaystyle 2^{3\cdot8-4}\leqslant10^{8-2}{\small , }\)
\(\displaystyle 2^{20}\leqslant10^6{\small , }\)
\(\displaystyle 1048576 \leqslant1 000 000 \) – дұрыс емес.
- \(\displaystyle n=9\) – қолайлы:
\(\displaystyle 2^{3\cdot 9-2}\leqslant10^{9-2}{\small , }\)
\(\displaystyle 2^{23}\leqslant10^7{\small , }\)
\(\displaystyle 8 388 608 \leqslant10 000 000 \) – дұрыс.
Демек, бұл тоғыз атыс (және, тиісінше, тоғыз оқ) атқышқа кем дегенде \(\displaystyle 0{,}84{\small}\) ықтималдықпен нысанаға тигізу үшін жеткілікті болады дегенді білдіреді.
Жауабы: \(\displaystyle 9{\small .}\)