Егер белгілі бір ауруға күдік болса, науқас ПТР-тестіне жіберіледі. Егер ауру шынымен болса, онда тест \(\displaystyle 72\%\) жағдайда оны растайды. Егер ауру болмаса, онда тест орташа \(\displaystyle 95\%\) жағдайда аурудың жоқтығын анықтайды. Тестілеуге жіберілген науқастардың \(\displaystyle 15\%\) орташа есеппен оң нәтиже беретіні белгілі. Белгілі бір науқасты тексеру кезінде дәрігер оны ПТР талдауына жіберді, ол оң нәтиже берді. Науқаста аурудың шын мәнінде болуы ықтималдығы қандай?
«Егер тест нәтижесі оң болса, науқас ауырады» оқиғасының ықтималдығын табыңыз:
нәтижені жүздікке дейін дөңгелектеңіз
Оқиғаларды белгілейік:
- \(\displaystyle A_1\) – науқас ауырады,
- \(\displaystyle A_2\) – науқастың дені сау,
- \(\displaystyle B_1\) – тест нәтижесі оң,
- \(\displaystyle B_2\) – тест нәтижесі теріс.
\(\displaystyle P(B_1)\) және \(\displaystyle P(B_2){\small}\) ықтималдықтарын есептейік:
- есеп шарты бойынша \(\displaystyle P(B_1)=0{,}15\) (сынақ нәтижесінің оң болу ықтималдығы);
- сонда \(\displaystyle P(B_2)=1-0{,}15=0{,}85\) (сынақ нәтижесінің теріс болу ықтималдығы).
Есеп шарты бойынша белгілі:
- Науқас ауырса, тесттің оң шығу ықтималдығы \(\displaystyle 0{,}72\small\) тең. Демек, науқас адамда теріс сынақтың ықтималдығы \(\displaystyle 1-0{,}72=0{,}28\small\) тең.
Яғни
\(\displaystyle P_{A_1}(B_1)=0{,}72\) ("науқас ауырған жағдайда, сынақ нәтижесі оң" шартты ықтималдығы);
\(\displaystyle P_{A_1}(B_2)=0{,}28 \) ("науқас ауырса, сынақ нәтижесі теріс" шартты ықтималдығы).
- Егер науқас сау болса, сынақ нәтижесі \(\displaystyle 0{,}95\small\) ықтималдығымен теріс болады, сондықтан сау адамда оң сынақтың ықтималдығы \(\displaystyle 1-0{,}95=0{,}05\small.\)
Яғни
\(\displaystyle P_{A_2}(B_2)=0{,}95\) ("науқас сау болса, сынақ нәтижесі теріс" шартты ықтималдығы);
\(\displaystyle P_{A_2}(B_1)=0{,}05\) ("науқас сау болса, сынақ нәтижесі оң" шартты ықтималдығы).
\(\displaystyle P(A_1)\) мәнін табамыз.
Ол үшін \(\displaystyle P(B_1){ \small }\) белгілі мәнін қолданамыз, оны жалпы ықтималдық формуласы бойынша жазамыз.
Белгілеуді енгізейік:
- \(\displaystyle P(A_1)=x\) (науқастың ауыру ықтималдығы) болсын;
- онда \(\displaystyle P(A_2)=1-x\) (науқастың сау болу ықтималдығы).
Түсінікті болу үшін \(\displaystyle B_1 \) оқиғасы үшін барлық ықтималдықтарды белгілейтін ықтимал нәтижелердің графигін құрайық:
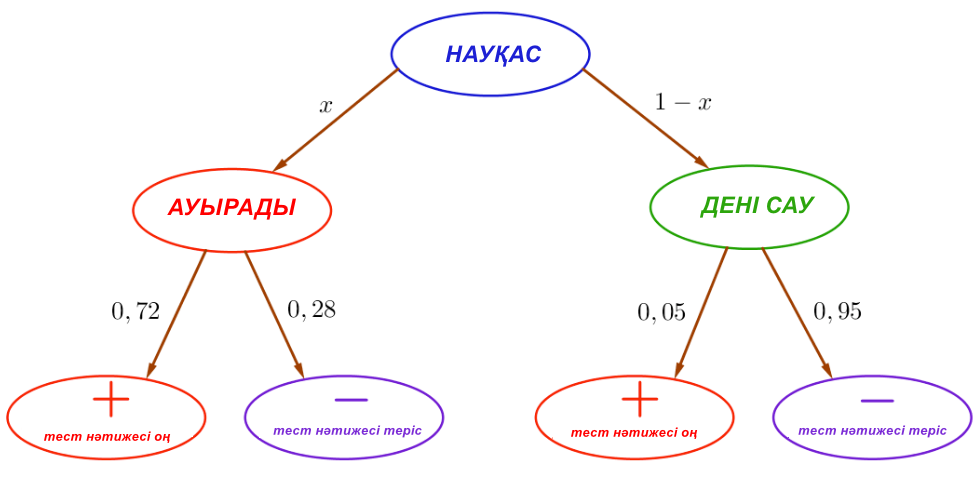
Графиктен біз екі жолдың оң сынақ үшін қолайлы екенін көреміз:
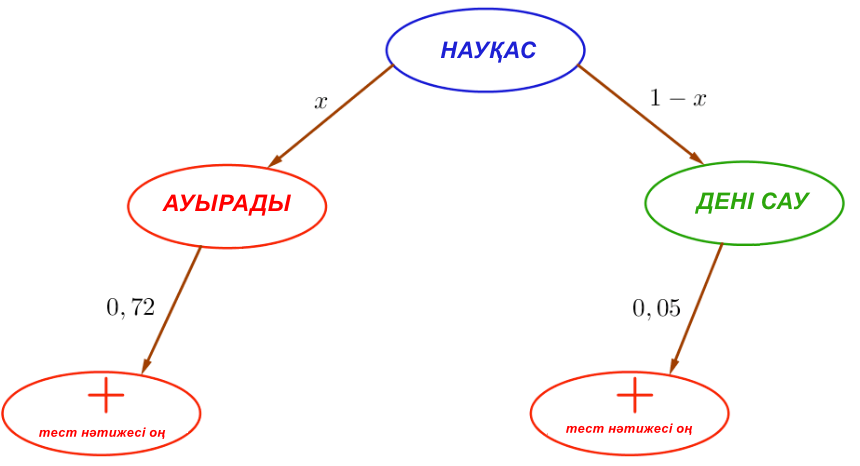
- Бірінші жол (графиктің сол тармағы) "науқас ауырды және сынама оң" оқиғасына сәйкес келеді. Осы оқиғаның ықтималдығын жазайық:
\(\displaystyle \\ \)\(\displaystyle P(\text{\scriptsize науқас ауырды және сынама нәтижесі оң})=\color{red}{P(A_1) \cdot P_{A_1}(B_1)} {\small.}\) \(\displaystyle \\ \)
- Екінші жол (графиктің оң тармағы) "науқастың дені сау және сынама оң" оқиғасына сәйкес келеді. Осы оқиғаның ықтималдығын жазайық:
\(\displaystyle \\ \) \(\displaystyle P(\text{\scriptsize науқастың дені сау және сынама нәтижесі оң})=\color{green}{P(A_2) \cdot P_{A_2}(B_1)} {\small.}\)
\(\displaystyle B_1\)(тест нәтижесі оң) оқиғасының жалпы ықтималдығы осы ықтималдықтардың қосындысына тең:
\(\displaystyle P(B_1)=\color{red}{P(A_1) \cdot P_{A_1}(B_1)}+\color{green}{P(A_2) \cdot P_{A_2}(B_1)} \small.\) \(\displaystyle \\ \)
Алынған формулаға сандық мәндерді қоямыз:
\(\displaystyle 0{,}15= x \cdot 0{,}72+(1-x) \cdot 0{,}05\small.\)
Бұл теңдеуді шешіп, \(\displaystyle x\small\) табамыз:
\(\displaystyle 0{,}15=0{,}72\cdot x+0{,}05-0{,}05\cdot x\small,\)
\(\displaystyle 0{,}67 \cdot x=0{,}1\small,\)
\(\displaystyle x=\frac{0{,}1}{0{,}67}=\frac{10}{67}\small.\)
Демек,
\(\displaystyle P(A_1)=\frac{10}{67}\small.\)
«Егер сынақтың нәтижесі оң болса, науқас ауырады» оқиғасының ізделінген ықтималдығын есептейміз.
Ол үшін «науқас ауырып жатыр және сынама оң нәтиже берді» = «сынама оң және науқас аурады» оқиғасын екі жолмен қарастырамыз:
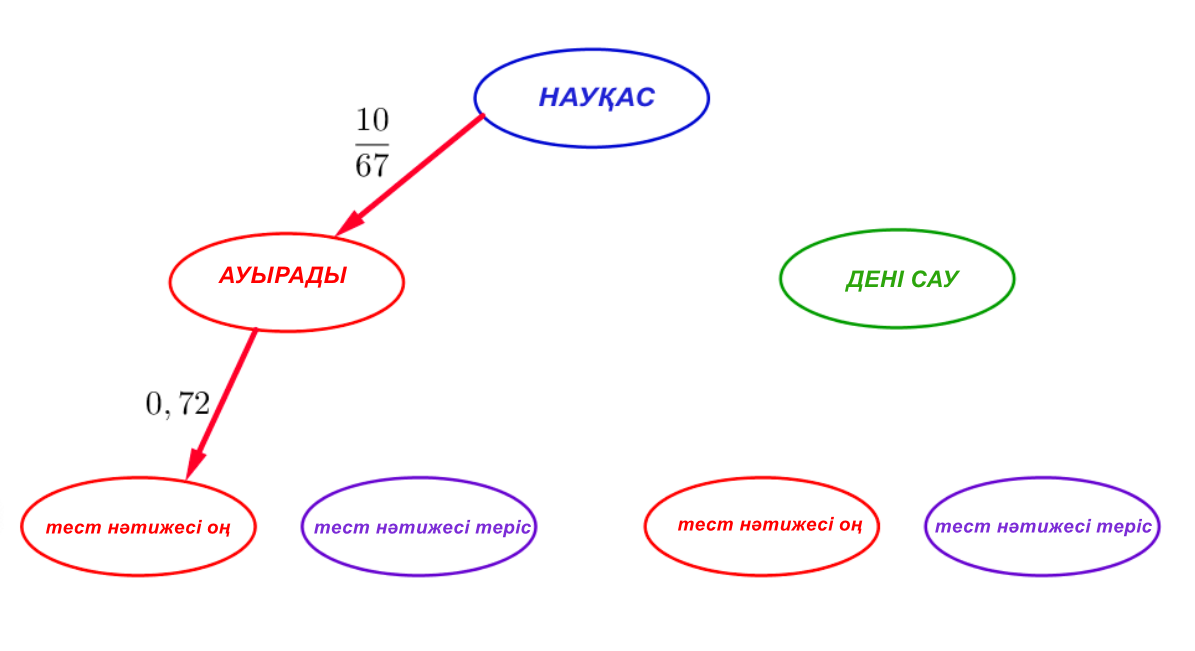 | 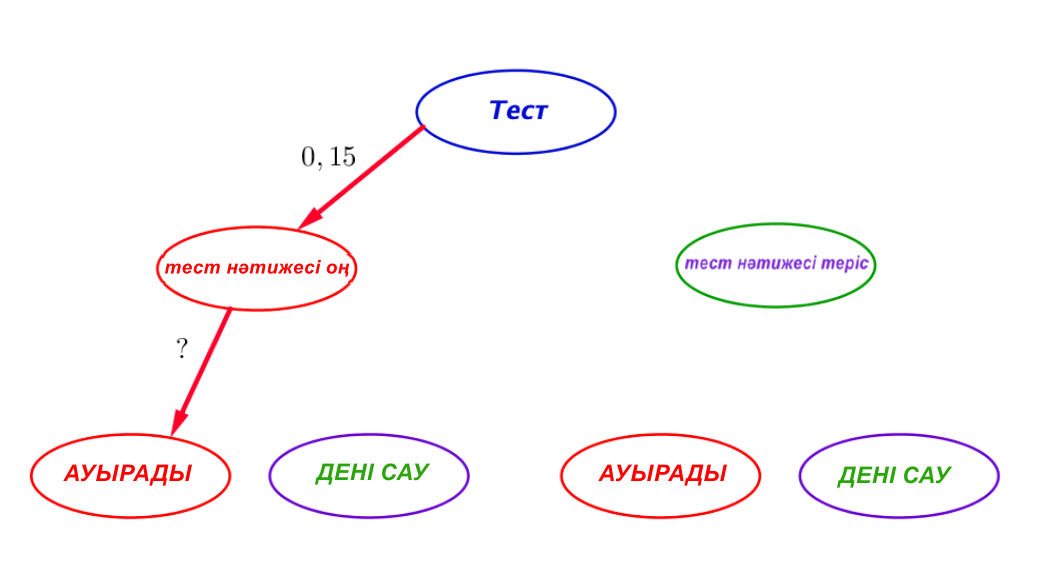 |
| \(\displaystyle \frac{10}{67} \cdot 0,72\) | \(\displaystyle 0,15 \cdot \Large{?} \) |
Келесіні аламыз:
\(\displaystyle \frac{10}{67} \cdot 0,72= 0,15 \cdot \Large{?}, \)
яғни
\(\displaystyle \frac{10}{67} \cdot 0,72= 0,15 \cdot P_{B_1}(A_1){\small,}\)
\(\displaystyle P_{B_1}(A_1)=\frac{10}{67} \cdot \frac{72}{100}:\frac{15}{100}\approx 0{,}72 {\small.}\)
Жауабы: \(\displaystyle 0{,}72 \small.\)