В ящике четыре красных и два синих фломастера. Фломастеры вытаскивают по очереди в случайном порядке. Какова вероятность того, что первый раз синий фломастер появится третьим по счету?
Пусть событие \(\displaystyle A\ - \) "первый раз синий фломастер появится третьим по счету".
Начнем строить граф возможных исходов, на котором:
- красной стрелкой обозначим элементарное событие "из ящика вытащили красный фломастер",
- синей стрелкой обозначим элементарное событие "из ящика вытащили синий фломастер".
Вероятности элементарных событий будем вычислять по формуле классической вероятности.
Формула классической вероятности
\(\displaystyle P(X)=\frac{\text{\small число благоприятных элементарных событий}}{\text{\small число всех элементарных событий}}\)
По условию задачи первым нужно вытащить красный фломастер.

Так как всего фломастеров \(\displaystyle 6\), из них \(\displaystyle 4\) фломастера красные, то это событие произойдет с вероятностью \(\displaystyle \frac{4}{6}\small.\)
Продолжим строить граф возможных исходов по благоприятной ветке и обозначим на нем найденную вероятность благоприятного события.
На втором шаге снова нужно вытащить красный фломастер.
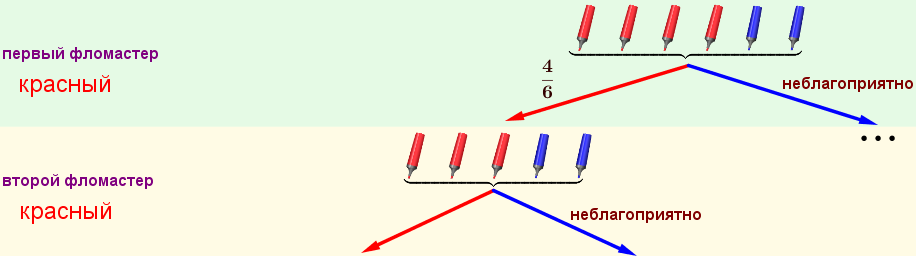
После того как на первом шаге вытащили красный фломастер, всего осталось \(\displaystyle 5\) фломастеров, из них \(\displaystyle 3\) красных. Значит, на втором шаге вероятность вытащить красный фломастер равна \(\displaystyle \frac{3}{5} \small.\)
Достроим граф возможных исходов по благоприятной ветке и обозначим на нем найденную вероятность.
На третьем шаге необходимо вытащить синий фломастер.
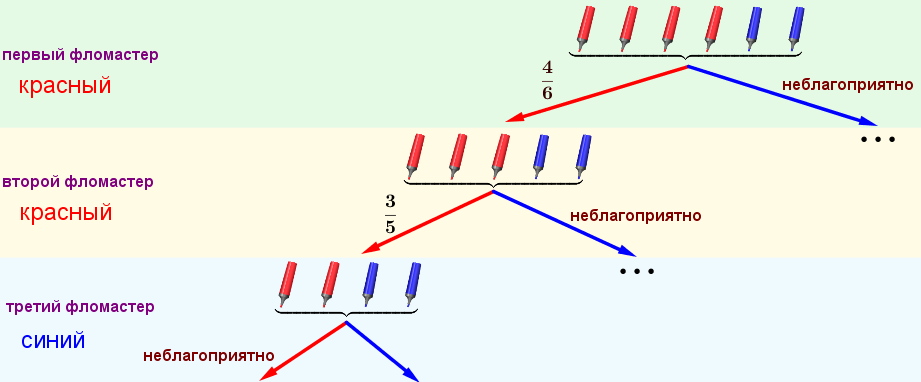
Осталось \(\displaystyle 4\) фломастера, из них \(\displaystyle 2\) синих. Значит, вероятность вытащить на третьем шаге синий фломастер будет равна \(\displaystyle \frac{2}{4}\small.\)
Обозначим на графе найденную вероятность и, для наглядности, уберем стрелки, соответствующие неблагоприятным исходам.
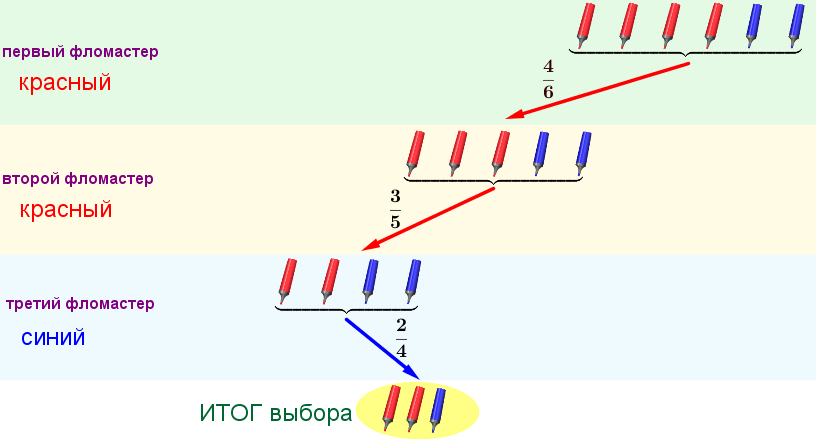
Событию \(\displaystyle A\) соответствует единственный путь на графе.
Вероятность одновременного наступления трех благоприятных непересекающихся исходов равна произведению их вероятностей.
Значит,
\(\displaystyle P(A)=\frac{4}{6} \cdot \frac{3}{5} \cdot \frac{2}{4}=\frac{1}{5}=0{,}2.\)
Ответ: \(\displaystyle 0{,}2.\)