Мерген бес бірдей нысанды атып тастайды. Әрбір нысанаға екіден көп емес ату беріледі және нысанаға әрбір жеке ату ықтималдығы \(\displaystyle 0{,}6{\small .}\) "Мерген дәл бес нысанды кесіп өтеді" оқиғасының ықтималдығы неше рет "мерген дәл төрт нысанды кесіп өтеді" оқиғасының ықтималдығынан жоғары?
Тапсырманы талдаймыз.
1. «Мерген нысанаға тиді» оқиғасының ықтималдығы мергеннің қандай нысанаға ататынына байланысты емес. Сонымен, бізде «Мерген нысанаға тиді» оқиғалары бірдей болуы мүмкін.
2. "Мерген бес нысанаға тиді" оқиғасы "мерген нысанаға түсті" бес тәуелсіз, бірдей ықтимал оқиғалардан тұрады. Яғни:
- бұл оқиғалардың ықтималдығының көбейтіндісі ретінде қарастырылады,
- нәтиже дәреже болады, өйткені біз бірдей ықтималдықты көбейтеміз.
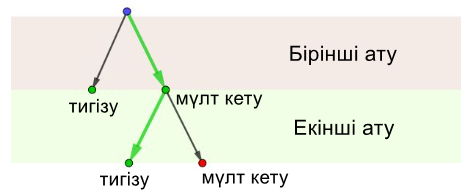
3. "Мерген бес нысанның дәл төрт нысанасына түсті" оқиғасы бес сәйкес емес нұсқаға бөлінеді:
Осы нұсқалардың әрқайсысы мыналардан тұрады:
- «мерген нысанаға тиді» төрт оқиғасынан;
- «мерген нысанаға тимеді» бір оқиғасынан.
Бұл жағдайда әр нұсқаның ықтималдығы бірдей.
Нұсқалар саны беске тең.
Әр тармақтың ықтималдығын есептейміз.
1. \(\displaystyle A \) арқылы нысанаға оқ тиген оқиғаны белгілейміз. Онда \(\displaystyle \overline{A} \) – нысанаға тимеді.
\(\displaystyle P(A)=p{\small }\) белгілейміз, онда \(\displaystyle P(\overline{A})=1-p=q{\small .}\)
2. Белгілерді қолдана отырып, келесілерді аламыз:
\(\displaystyle P(AAAAA)=P(A)\cdot P(A)\ldots \cdot P(A)=(P(A))^5=p^5{\small .}\)
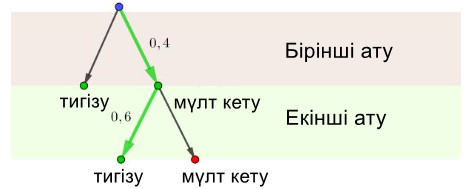
3. Жазбаларды қолдана отырып, біз әр нұсқаның ықтималдығын есептейміз. Ол үшін бірінші нұсқаның ықтималдығын есептеу жеткілікті:
\(\displaystyle P(AAAA\overline{A})= P(A)\cdot P(A)\cdot P(A)\cdot P(A)\cdot P(\overline{A})=p^4q{\small .}\)
Сонда
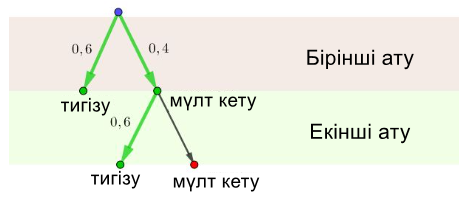
\(\displaystyle P(\text{\scriptsize "мерген бес нысананың төртеуіне дәл тиді"})=\underbrace{p^4q+\ldots+p^4q}_{ 5\, рет}=5p^4q{\small .}\)
\(\displaystyle p=P(A)\) – бір нысанаға түсіру ықтималдығын табамыз.
Сонда
\(\displaystyle q=1-p=1-0{,}84=0{,}16{\small .}\)
Табылған мәндерді ықтималдыққа қоямыз.
Төмендегіні аламыз:
\(\displaystyle P(\text{\scriptsize"мерген бес нысананаға дәл тиді"})=p^5=(0{,}84)^5{\small ;}\)
\(\displaystyle P(\text{\scriptsize"мерген бес нысананың төртеуіне дәл тиді"})=5p^4q =5\cdot 0{,}16\cdot (0{,}84)^4{\small .}\)
"Мерген бес нысананаға дәл тиді" оқиғасының ықтималдығы "мерген төрт нысананаға дәл тиді" оқиғасының ықтималдығынан неше есе жоғары екенін табамыз:
\(\displaystyle \frac{P(\text{\scriptsize"мерген бес нысананаға дәл тиді"})}{P(\text{\scriptsize"мерген бес нысананың төртеуіне дәл тиді"})}=\frac{(0{,}84)^5}{5\cdot 0{,}16\cdot (0{,}84)^4}=\frac{0{,}84}{5\cdot 0{,}16}=\frac{0{,}84}{ 0{,}8}=1{,}05{\small .}\)
Жауабы: \(\displaystyle 1{,}05{\small .}\)