Теңбүйірлі трапецияның табандары \(\displaystyle 6\) және \(\displaystyle 12.\) Трапецияның сүйір бұрышының синусы \(\displaystyle 0{,}8\small.\) Трапецияның ауданын табыңыз.
\(\displaystyle ABCD\small\) теңбүйірлі трапециясының \(\displaystyle AD=12\) және\(\displaystyle BC=6\) табандары \(\displaystyle AB=CD\) бүйір қабырғалары болсын. Теңбүйірлі трапецияның қасиеті бойынша табанындағы бұрыштары тең. Демек, \(\displaystyle \sin \angle A=\sin \angle D =0{,}8\small.\) Трапецияның ауданын табу керек. \(\displaystyle ABCD\small\) трапециясының \(\displaystyle BH \) және\(\displaystyle CK \) биіктіктерін жүргіземіз | 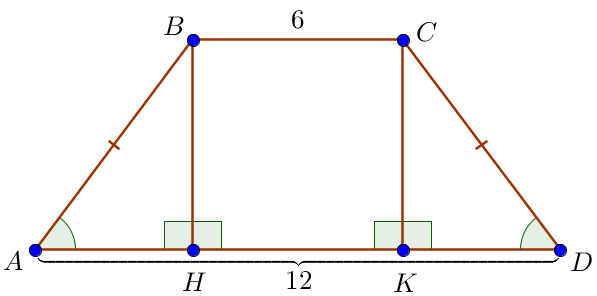 |
Трапецияның табандары параллель және трапецияның биіктіктері табандарына перпендикуляр болғандықтан , \(\displaystyle BH K C \) – тіктөртбұрыш. Сонда \(\displaystyle H K =BC=6 \small.\)
\(\displaystyle ABH\) және \(\displaystyle DCK\) тікбұрышты үшбұрыштары \(\displaystyle AB=CD\) гипотенузалары және \(\displaystyle BH=CK\small\) катеттері бойынша тең. Демек, \(\displaystyle AH=DK\) және \(\displaystyle AH=DK=\frac{AD-BC}{2}\small,\) \(\displaystyle AH=\frac{12-6}{2}=\frac{6}{2}=3\small.\) | 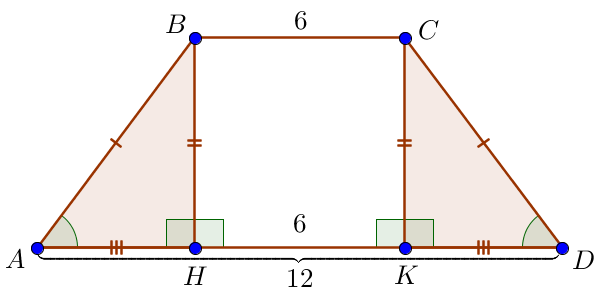 |
\(\displaystyle ABH\small\) тікбұрышты үшбұрышынан трапецияның \(\displaystyle BH \) биіктігін табамыз \(\displaystyle \sin \angle BAH=0{,}8\) және \(\displaystyle BAH\) сүйір бұрышына іргелес катет \(\displaystyle AH=3\small\) белгілі Негізгі тригонометриялық сәйкестікке сәйкес \(\displaystyle \begin{aligned}\cos ^2 \angle BAH &=1- \sin ^2 \angle BAH=\\ &=1- (0{,}8)^2=1-0{,}64=0{,}36\small. \end{aligned}\) \(\displaystyle BAH\) бұрышы сүйір болғандықтан, оның косинусы оң болады: \(\displaystyle \cos \angle BAH =\sqrt{0{,}36}=0{,}6\small,\) \(\displaystyle \tg \angle BAH =\frac{\sin \angle BAH}{\cos \angle BAH} =\frac{0{,}8}{0{,}6}=\frac{4}{3}\small.\)
\(\displaystyle \tg \angle BAH =\frac{BH}{AH}\small\) болғандықтан, онда \(\displaystyle BH={AH}\cdot {\tg \angle BAH}={3}\cdot {\frac{4}{3}}=4\small.\) | 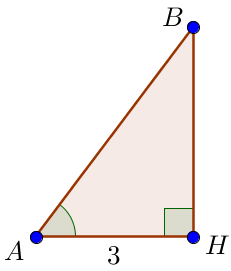 |
Трапецияның ауданы табандарының қосындысының жартысының мен биіктігінің көбейтіндісіне тең болғандықтан, онда
\(\displaystyle S_{ABCD}=\frac{AD+BC}{2}\cdot BH=\frac{12+6}{2}\cdot 4=\frac{18}{2}\cdot 4={9}\cdot 4=36\small.\)
Жауабы: \(\displaystyle 36 \small.\)