Теңбүйірлі трапецияның табандары \(\displaystyle 43 \) және \(\displaystyle 73 . \) Трапецияның сүйір бұрышының косинусы \(\displaystyle \dfrac{5}{7}\small.\) Бүйір қабырғасын табыңыз.
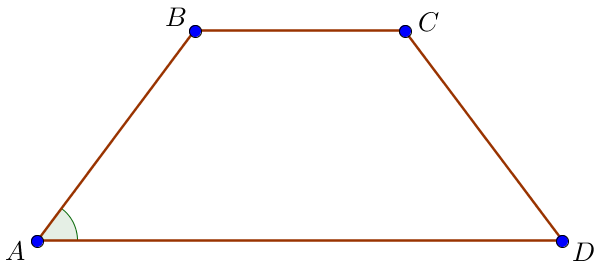
\(\displaystyle ABCD\small\) теңбүйірлі трапециясының \(\displaystyle AD=73\) және \(\displaystyle BC=43\) табандары \(\displaystyle AB=CD\) бүйір қабырғалары болсын. Теңбүйірлі трапецияның қасиеті бойынша табанындағы бұрыштары тең. Демек, \(\displaystyle \cos \angle A=\cos \angle D=\frac{5}{7}\small.\) Бүйір қабырғасын табу керек. Трапецияның \(\displaystyle BH \) және \(\displaystyle CK \) биіктіктерін жүргіземіз. | 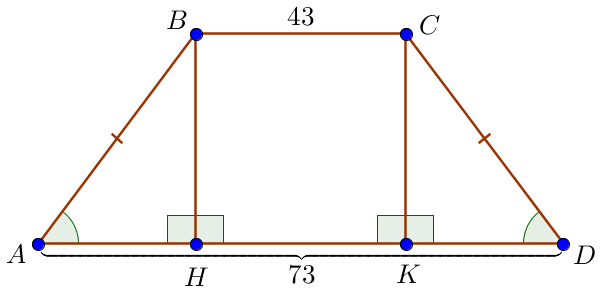 |
Трапецияның табандары параллель және трапецияның биіктіктері табандарына перпендикуляр болғандықтан , \(\displaystyle BH K C \) – тік төртбұрыш. Сонда \(\displaystyle H K =BC=43 \small.\)
\(\displaystyle ABH\) және \(\displaystyle DCK\) тікбұрышты үшбұрыштары \(\displaystyle AB=CD\) гипотенузалары және \(\displaystyle BH=CK\small\) катеттері бойынша тең. Демек \(\displaystyle AH=DK\) және \(\displaystyle AH=DK=\frac{AD-BC}{2}\small,\) \(\displaystyle AH=\frac{73-43}{2}=\frac{30}{2}=15\small.\) |  |
\(\displaystyle ABH\small\) үшбұрышынан трапецияның \(\displaystyle AB \) бүйір қабырғасын табамыз . Бізге \(\displaystyle \cos \angle BAH=\frac{5}{7}\) және \(\displaystyle BAH\) сүйір бұрышына іргелес катеті \(\displaystyle AH=15\small\) белгілі демек \(\displaystyle \cos \angle BAH=\frac{AH}{AB},\) онда \(\displaystyle AB=\frac{AH}{\cos\angle BAH}=\frac{15}{\phantom{1}{\displaystyle\frac{5}{7}}\phantom{1}}=\) \(\displaystyle =\frac{15\cdot 7}{5}=3\cdot 7=21\small.\) | 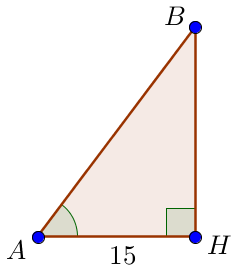 |
Жауабы: \(\displaystyle 21 \small.\)