Теориясы: 03 Аудан

\(\displaystyle a)\) Есептің шарты бойынша сызбаны орындайық.

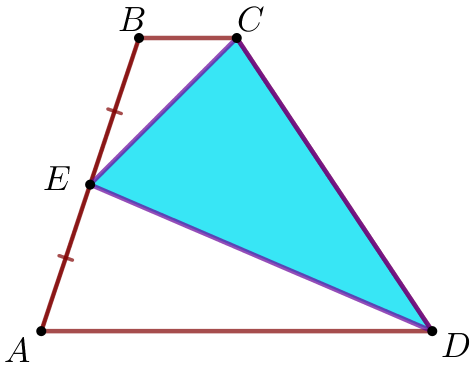\(\displaystyle ABCD\) – трапеция; \(\displaystyle E\) – нүктесі \(\displaystyle AB{\small,}\) қабырғасының ортасы яғни \(\displaystyle AE=BE{\small.}\)    \(\displaystyle ECD\) үшбұрышының ауданы трапеция ауданының жартысына тең екенін дәлелдеу қажет.

Правило

Ауданның қасиеті

Егер көпбұрыш бірнеше көпбұрыштардан тұрса (бір-бірімен қабаттаспайтын), онда оның ауданы осы көпбұрыштардың аудандарының қосындысына тең болады.

\(\displaystyle S=S_1+S_2+S_3+S_4\)

төмендегіні аламыз

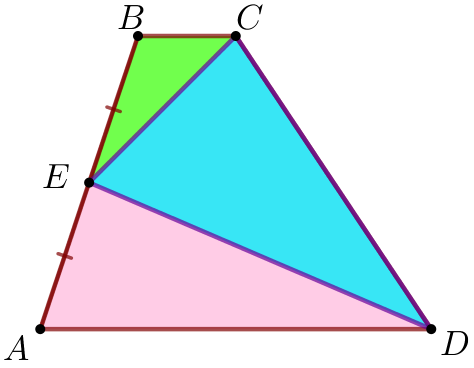Трапеция үш үшбұрыштан тұратындықтан, трапецияның ауданы осы үшбұрыштардың аудандарының қосындысына тең: \(\displaystyle S_{ABCD}=S_{\triangle ECD}+S_{\triangle BEC}+S_{\triangle AED}{\small.}\) Сонда \(\displaystyle S_{\triangle ECD}=S_{ABCD}-(S_{\triangle BEC}+S_{\triangle AED}){\small.}\)

 \(\displaystyle ABCD {\small}\) трапециясының ауданы арқылы \(\displaystyle BEC\) және \(\displaystyle AED\) үшбұрыштарының аудандарының қосындысын өрнектейік

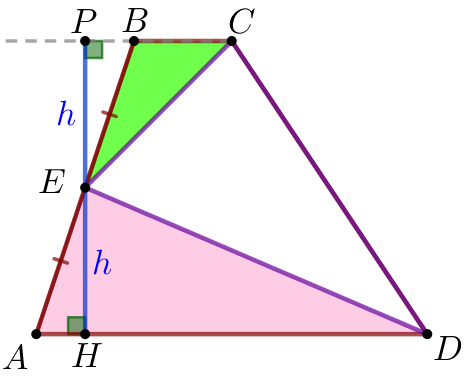
Қосымша сызбаны орындайық.

\(\displaystyle E\) нүктесі арқылы трапеция табандарына перпендикуляр жүргіземіз \(\displaystyle P\) және \(\displaystyle H\) әріптерімен перпендикулярдың сәйкесінше \(\displaystyle BC\) және \(\displaystyle AD\) түзулерімен қиылысу нүктелерін белгілейік.  \(\displaystyle BEP\) және \(\displaystyle AEH{\small}\) тікбұрышты үшбұрыштарын қарастырайық \(\displaystyle BE=AE \) (шарт бойынша); \(\displaystyle \angle BEP=\angle AEH \)(тік бұрыштар). Демек,  \(\displaystyle \triangle BEP=\triangle AEH\) гипотенуза және сүйір бұрыш бойынша.

Тең үшбұрыштарда сәйкес қабырғалар тең болады. Яғни,

\(\displaystyle EP=EH=h {\small.}\)

Правило

Үшбұрыштың аудан формуласы

Үшбұрыштың \(\displaystyle S\) ауданы \(\displaystyle a\) қабырғасының осы қабырғаға жүргізілген биіктікке \(\displaystyle h{\small}\) көбейтіндісінің жартысына тең::

\(\displaystyle S=\frac{1}{2} \cdot a \cdot h {\small,}\) мұндағы \(\displaystyle a\) – үшбұрыштың қабырғасы, \(\displaystyle h\) – үшбұрыштың биіктігі.

\(\displaystyle S_{\triangle BEC}=\frac{1}{2} \cdot BC \cdot h {\small;}\\ \) \(\displaystyle S_{\triangle AED}=\frac{1}{2} \cdot AD\cdot h {\small;}\)

Сонда

\(\displaystyle S_{\triangle BEC}+S_{\triangle AED}=\frac{1}{2} \cdot BC \cdot h +\frac{1}{2} \cdot AD\cdot h{\small;}\\ \)

\(\displaystyle S_{\triangle BEC}+S_{\triangle AED}=\frac{1}{2} \cdot h \cdot (BC+AD){\small;}\\ \)

\(\displaystyle S_{\triangle BEC}+S_{\triangle AED}=\frac{ (BC+AD)}{2} \cdot h{\small.}\)

Правило

Трапеция ауданы

Трапецияның ауданы биіктікке табандарының жарты қосындысының көбейтіндісіне тең.

\(\displaystyle S=\frac{\color{blue}{a}+\color{blue}{b}}{2}\cdot \color{red}{h}\)

Біздің жағдайда  

\(\displaystyle PH\) – трапецияның биіктігі, \(\displaystyle BC\) және \(\displaystyle AD\) – трапеция табандары. Яғни,

\(\displaystyle S_{ABCD}=\frac{BC+AD}{2} \cdot PH {\small.}\)

Себебі \(\displaystyle PH=EP+EH=h+h=2 \cdot h {\small}\) болғандықтан, онда

\(\displaystyle S_{ABCD}=\frac{BC+AD}{2} \cdot 2 \cdot h {\small.}\)

Яғни, 

\(\displaystyle S_{\triangle BEC}+S_{\triangle AED}=\frac{1}{2} \cdot S_{ABCD} {\small.}\)

Сонда

\(\displaystyle S_{\triangle ECD}=S_{ABCD}-(S_{\triangle BEC}+S_{\triangle AED}){\small;}\\ \)

\(\displaystyle S_{\triangle ECD}=S_{ABCD}-\frac{1}{2} \cdot S_{ABCD}{\small.}\\ \)

\(\displaystyle S_{\triangle ECD}=\frac{1}{2} \cdot S_{ABCD}{\small.}\\ \)

Яғни  \(\displaystyle ECD\) үшбұрышының ауданы трапеция ауданының жартысына тең.

Тұжырым дәлелденді.

\(\displaystyle б) \) Есептің шарты бойынша \(\displaystyle S_{ABCD}=54 {\small.}\)

 \(\displaystyle BEC\) және \(\displaystyle AED {\small}\) үшбұрыштары аудандарының қосындысын табу қажет

 \(\displaystyle a)\) тармағында \(\displaystyle BEC\) және \(\displaystyle AED \) үшбұрыштары аудандарының қосындысы \(\displaystyle ABCD{\small}\) трапеция ауданының жартысына тең екенін алдық

\(\displaystyle S_{\triangle BEC}+S_{\triangle AED}=\frac{1}{2} \cdot S_{ABCD} {\small;}\\ \)

\(\displaystyle S_{\triangle BEC}+S_{\triangle AED}=\frac{1}{2} \cdot 54=27 {\small.}\)

Жауабы: \(\displaystyle б) \ 27{\small.} \)