Задание
Выберите координату \(\displaystyle x{\small ,}\) в которой значение функции \(\displaystyle y=-\frac{1}{2}x^2\) будет наибольшим.
Решение
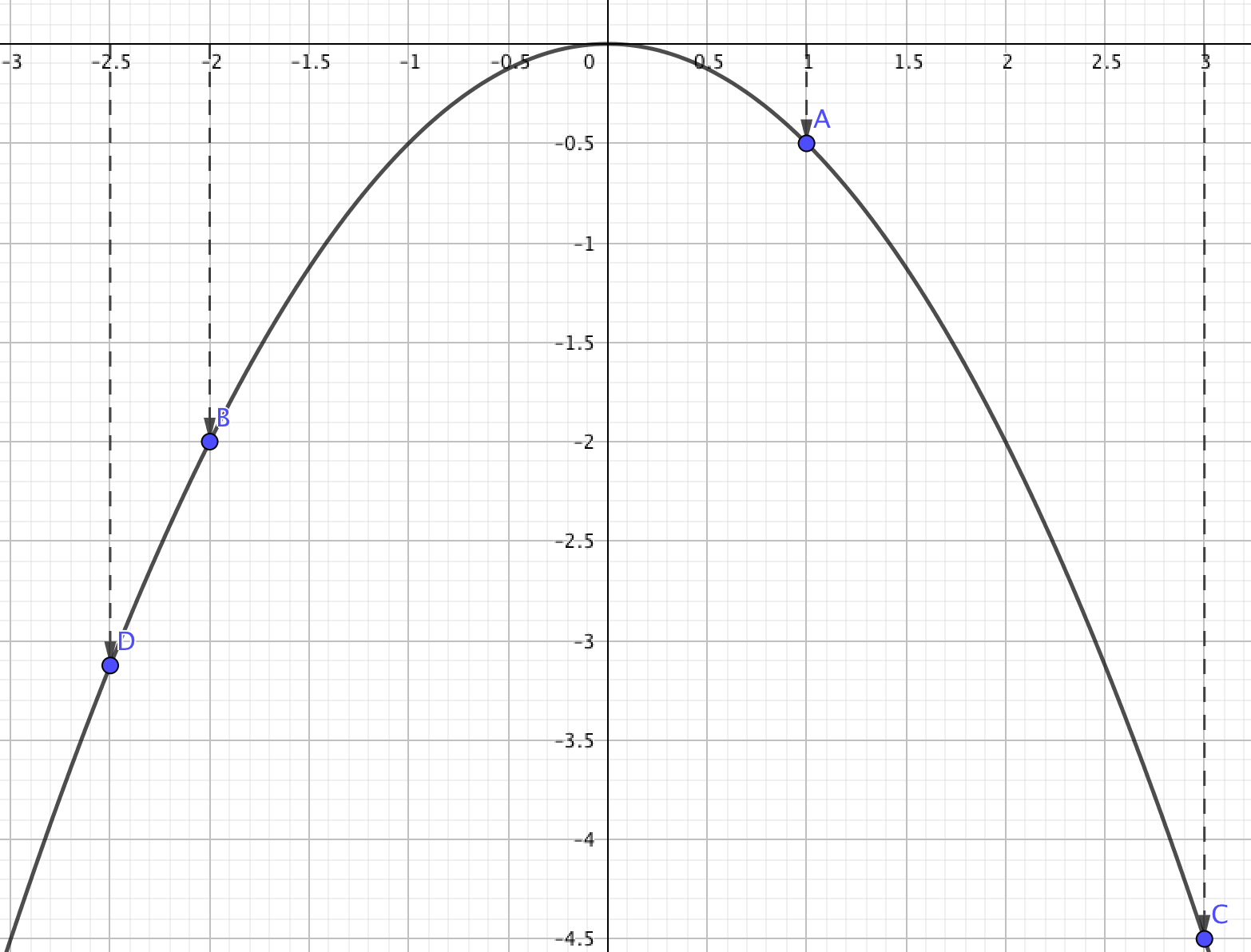
Значению функции в точке \(\displaystyle x=a\) соответствует координата \(\displaystyle y\) точки, лежащей на графике данной функции с координатой \(\displaystyle x=a{\small .}\)
Определим положение координаты \(\displaystyle y\) каждой из данных точек:
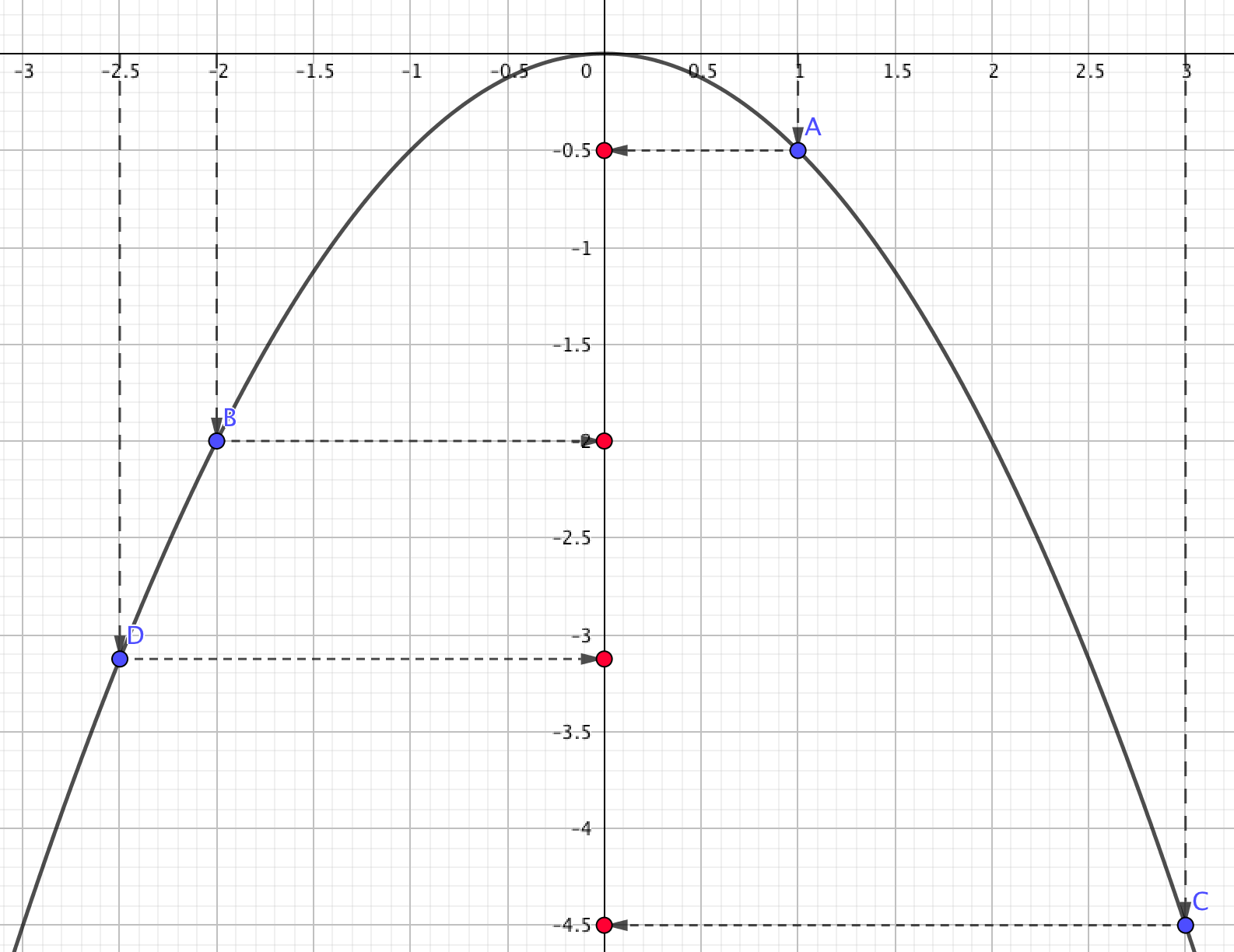
Из чертежа следует, что наибольшее значение \(\displaystyle y\) имеет точка с координатой \(\displaystyle x=1{\small .}\)
Таким образом, из данных значений переменной \(\displaystyle x\) при \(\displaystyle x=1\) значение функции \(\displaystyle y=-\frac{1}{2}x^2\) будет наибольшим.
Ответ: \(\displaystyle x=1{\small .}\)